
 湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).
湖州素有鱼米之乡之称,某水产养殖大户为了更好地发挥技术优势,一次性收购了20000kg淡水鱼,计划养殖一段时间后再出售.已知每天放养的费用相同,放养10天的总成本为30.4万元;放养20天的总成本为30.8万元(总成本=放养总费用+收购成本).分析 (1)由放养10天的总成本为30.4万元;放养20天的总成本为30.8万元可得答案;
(2)①分0≤t≤50、50<t≤100两种情况,结合函数图象利用待定系数法求解可得;
②就以上两种情况,根据“利润=销售总额-总成本”列出函数解析式,依据一次函数性质和二次函数性质求得最大值即可得.
解答 解:(1)由题意,得:$\left\{\begin{array}{l}{10a+b=30.4}\\{20a+b=30.8}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=0.04}\\{b=30}\end{array}\right.$,
答:a的值为0.04,b的值为30;
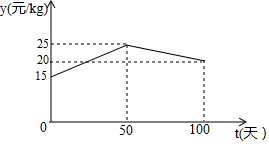
(2)①当0≤t≤50时,设y与t的函数解析式为y=k1t+n1,
将(0,15)、(50,25)代入,得:$\left\{\begin{array}{l}{{n}_{1}=15}\\{50{k}_{1}+{n}_{1}=25}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{1}=\frac{1}{5}}\\{{n}_{1}=15}\end{array}\right.$,
∴y与t的函数解析式为y=$\frac{1}{5}$t+15;
当50<t≤100时,设y与t的函数解析式为y=k2t+n2,
将点(50,25)、(100,20)代入,得:$\left\{\begin{array}{l}{50{k}_{2}+{n}_{2}=25}\\{100{k}_{2}+{n}_{2}=20}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{{k}_{2}=-\frac{1}{10}}\\{{n}_{2}=30}\end{array}\right.$,
∴y与t的函数解析式为y=-$\frac{1}{10}$t+30;
②由题意,当0≤t≤50时,
W=20000($\frac{1}{5}$t+15)-(400t+300000)=3600t,
∵3600>0,
∴当t=50时,W最大值=180000(元);
当50<t≤100时,W=(100t+15000)(-$\frac{1}{10}$t+30)-(400t+300000)
=-10t2+1100t+150000
=-10(t-55)2+180250,
∵-10<0,
∴当t=55时,W最大值=180250(元),
综上所述,放养55天时,W最大,最大值为180250元.
点评 本题主要考查二次函数的应用,熟练掌握待定系数法求函数解析式,根据相等关系列出利润的函数解析式及二次函数的性质是解题的关键.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:选择题
| A. | x>-1 | B. | x>3 | C. | -1<x<3 | D. | x<3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com