
【题目】如图,直线AB、CD相交于点O,∠BOM=90°,∠DON=90°.
(1)若∠COM=∠AOC,求∠AOD的度数;
(2)若∠COM=![]() ∠BOC,求∠AOC和∠MOD.
∠BOC,求∠AOC和∠MOD.

【答案】(1)135°(2)150°
【解析】分析:(1)根据∠COM=∠AOC可得∠AOC=![]() ∠AOM,再求出∠AOM的度数,然后可得答案;(2)设∠COM=x°,则∠BOC=4x°,进而可得∠BOM=3x°,从而可得3x=90,然后可得x的值,进而可得∠AOC和∠MOD的度数.
∠AOM,再求出∠AOM的度数,然后可得答案;(2)设∠COM=x°,则∠BOC=4x°,进而可得∠BOM=3x°,从而可得3x=90,然后可得x的值,进而可得∠AOC和∠MOD的度数.
本题解析:(1)∵∠COM=∠AOC,
∴∠AOC=![]() ∠AOM,
∠AOM,
∵∠BOM=90°,
∴∠AOM=90°,
∴∠AOC=45°,
∴∠AOD=180°﹣45°=135°;
(2)设∠COM=x°,则∠BOC=4x°,
∴∠BOM=3x°,
∵∠BOM=90°,
∴3x=90,即x=30,
∴∠AOC=60°,∠MOD=90°+60°=150°.


 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象相交于A、B两点。
的图象相交于A、B两点。

(1)利用图中条件,求反比例函数和一次函数的解析式
(2)根据图象写出使一次函数的值大于反比例函数的值的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了增强学生的身体素质,某校坚持常年的全员体育锻炼,并定期进行体能测试.下面将某班学生立定跳远成绩(精确到0.1m)进行整理后,分成5组(含低值不含高值):1.60~1.80,1.80~2.00,2.00~2.20,2.20~2.40,2.40~2.60,已知前4个小组的频率分别是0.05,0.15,0.30,0.35,第五个小组的频数是9.
(1)该班参加这项测试的人数是多少人?
(2)请画出频数分布直方图.
(3)成绩在2.00米以上(含2.00米)为合格,则该班成绩的合格率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工程由甲乙两队合做![]() 天完成,厂家需付甲乙两队共
天完成,厂家需付甲乙两队共![]() 元;乙丙两队合做
元;乙丙两队合做![]() 天完成,厂家需付乙丙两队共
天完成,厂家需付乙丙两队共![]() 元;甲丙两队合做
元;甲丙两队合做![]() 天完成全部工程的
天完成全部工程的![]() ,厂家需付甲丙两队共
,厂家需付甲丙两队共![]() 元.
元.
(1)求甲、乙、丙各队单独完成全部工程各需多少天?
(2)若要求不超过![]() 天完成全啊工程,问可由哪队单独完成此项工程花钱最少?
天完成全啊工程,问可由哪队单独完成此项工程花钱最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C,D分别在两个半圆上(不与点A、B重合),AD、BD的长分别是关于x的方程![]() =0的两个实数根.
=0的两个实数根.
(1)求m的值;
(2)连接CD,试探索:AC、BC、CD三者之间的等量关系,并说明理由;
(3)若CD=![]() ,求AC、BC的长.
,求AC、BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,∠ABK的角平分线BE的反向延长线和∠DCK的角平分线CF的反向延长线交于点H,∠K﹣∠H=27°,则∠K=( )
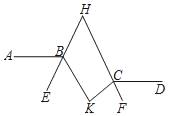
A. 76° B. 78° C. 80° D. 82°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB∥CD,C在D的右侧,BE平分∠ABC,DE平分∠ADC,BE、DE所在直线交于点E,∠ADC=70°.
(1)求∠EDC的度数;
(2)若∠ABC=n°,求∠BED的度数(用含n的代数式表示);
(3)将线段BC沿DC方向平移,使得点B在点A的右侧,其他条件不变,画出图形并判断∠BED的度数是否改变,若改变,求出它的度数(用含n的式子表示);若不改变,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com