
分析 (1)由题意可得y=x2+$\frac{1}{{x}^{2}}$≥2•x•$\frac{1}{x}$=2,即可求得答案;
(2)首先设无人机信号所在点的坐标为(x,$\frac{2}{x}$),则可得无人机与雷达站距离为:y=$\sqrt{{x}^{2}+({\frac{2}{x})}^{2}}$,然后根据题意求得答案;
(3)由并联后总电阻$\frac{1}{{R}_{并}}$=$\frac{1}{{R}_{1}}$+$\frac{1}{{R}_{2}}$,若R串=k•R并,可得k=$\frac{{R}_{串}}{{R}_{并}}$=$\frac{({R}_{1}+{R}_{2})^{2}}{{R}_{1}{R}_{2}}$,继而可得k=$\frac{{R}_{1}^{2}+{R}_{2}^{2}}{{R}_{1}{R}_{2}}$+2≥$\frac{2{R}_{1}{R}_{2}}{{R}_{2}{R}_{2}}$+2,继而求得答案.
解答 解:(1)∵y=x2+$\frac{1}{{x}^{2}}$≥2•x•$\frac{1}{x}$=2,
∴函数y=x2+$\frac{1}{{x}^{2}}$的最小值是2.
故答案为:2.
(2)设无人机信号所在点的坐标为(x,$\frac{2}{x}$),
则无人机与雷达站距离为:y=$\sqrt{{x}^{2}+({\frac{2}{x})}^{2}}$=$\sqrt{{x}^{2}+\frac{2}{{x}^{2}}}$≥$\sqrt{2•x•\frac{2}{x}}$=2,
当且仅当x=$\frac{2}{x}$时,即x=$\sqrt{2}$时,y有最小值为2.
∴无人机信号所在点的坐标为($\sqrt{2}$,$\sqrt{2}$).
(3)∵$\frac{1}{{R}_{并}}$=$\frac{1}{{R}_{1}}$+$\frac{1}{{R}_{2}}$=$\frac{{R}_{1}+{R}_{2}}{{R}_{1}{R}_{2}}$,
∴R并=$\frac{{R}_{1}{R}_{2}}{{R}_{1}+{R}_{2}}$,
∴k=$\frac{{R}_{串}}{{R}_{并}}$=$\frac{({R}_{1}+{R}_{2})^{2}}{{R}_{1}{R}_{2}}$=$\frac{{R}_{1}^{2}+{R}_{2}^{2}+2{R}_{1}{R}_{2}}{{R}_{1}{R}_{2}}$=$\frac{{R}_{1}^{2}+{R}_{2}^{2}}{{R}_{1}{R}_{2}}$+2≥$\frac{2{R}_{1}{R}_{2}}{{R}_{2}{R}_{2}}$+2=4,
∴k的取值范围为k≥4.
点评 此题属于反比例函数综合题,考查了几何不等式的应用.理解对于任意实数a、b,都有a2+b2≥2ab(当且仅当a=b时取等号)是关键.


科目:初中数学 来源: 题型:填空题
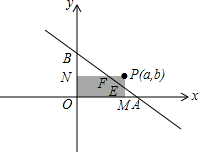 如图,点P(a,b)是第一象限内一点,若满足2ab=1,直线y=-x+1交x轴于点A,交y轴于点B,过点P作PM⊥x轴于点M,作PN⊥y轴于点N,直线y=-x+1分别交PM、PN于点E,F,则AF•BE的值是1.
如图,点P(a,b)是第一象限内一点,若满足2ab=1,直线y=-x+1交x轴于点A,交y轴于点B,过点P作PM⊥x轴于点M,作PN⊥y轴于点N,直线y=-x+1分别交PM、PN于点E,F,则AF•BE的值是1.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 20m | B. | 25m | C. | 30m | D. | 35m |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 邻边对应成比例的两个平行四边形 | B. | 有一条边相等的两个矩形 | ||
| C. | 有一个内角相等的两个菱形 | D. | 底角相等的两个等腰梯形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 将两个完全相同的等腰直角三角形摆成如图的样子,假设图形中的所有点、线都在同一个平面内,两个三角形的重叠部分为△ADE,则图中有与△ADE相似的三角形吗?请找出来,并说明理由.
将两个完全相同的等腰直角三角形摆成如图的样子,假设图形中的所有点、线都在同一个平面内,两个三角形的重叠部分为△ADE,则图中有与△ADE相似的三角形吗?请找出来,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
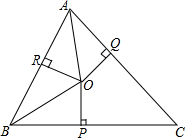 如图,已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.
如图,已知在△ABC中,∠A、∠B的角平分线交于点O,过O作OP⊥BC于P,OQ⊥AC于Q,OR⊥AB于R,AB=7,BC=8,AC=9.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com