
【题目】实验探究:
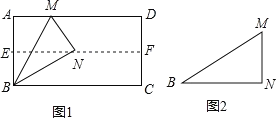
(1)如图1,对折矩形纸片ABCD,使AD与BC重合,得到折痕EF,把纸片展开;再一次折叠纸片,使点A落在EF上,并使折痕经过点B,得到折痕BM,同时得到线段BN,MN.请你观察图1,猜想∠MBN的度数是多少,并证明你的结论.
(2)将图1中的三角形纸片BMN剪下,如图2,折叠该纸片,探究MN与BM的数量关系,写出折叠方案,并结合方案证明你的结论.
【答案】(1)见解析;(2)见解析.
【解析】
(1)猜想:∠MBN=30°.只要证明△ABN是等边三角形即可;
(2)结论:MN=![]() BM.折纸方案:如图,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.由折叠可知△MOP≌△MNP,只要证明△MOP≌△BOP,即可推出MO=BO=
BM.折纸方案:如图,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.由折叠可知△MOP≌△MNP,只要证明△MOP≌△BOP,即可推出MO=BO=![]() BM;
BM;
(1)猜想:∠MBN=30.
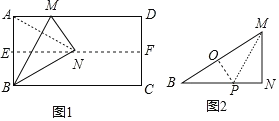
理由:如图1中,连接AN,∵直线EF是AB的垂直平分线,
∴NA=NB,
由折叠可知,BN=AB,
∴AB=BN=AN,
∴△ABN是等边三角形,
∴∠ABN=60,
∴NBM=∠ABM=![]() ∠ABN=30.
∠ABN=30.
(2)结论:MN=![]() BM.
BM.
折纸方案:如图2中,折叠△BMN,使得点N落在BM上O处,折痕为MP,连接OP.
理由:由折叠可知△MOP≌△MNP,
∴MN=OM,∠OMP=∠NMP=![]() ∠OMN=30=∠B,
∠OMN=30=∠B,
∠MOP=∠MNP=90,
∴∠BOP=∠MOP=90,
∵OP=OP,
∴△MOP≌△BOP,
∴MO=BO=![]() BM,
BM,
∴MN=![]() BM.
BM.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图,A(-5,0),B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB.∠CDA=90°.点P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时时间t秒.

(1)求点C的坐标;
(2)当∠BCP=15°时,求t的值;
(3)以点P为圆心,PC为半径的⊙P随点P的运动而变化,当⊙P与四边形ABCD的边(或边所在的直线)相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图A在数轴上所对应的数为﹣2.
![]()
(1)点B在点A右边距A点4个单位长度,求点B所对应的数;
(2)在(1)的条件下,点A以每秒2个单位长度沿数轴向左运动,点B以每秒2个单位长度沿数轴向右运动,当点A运动到﹣6所在的点处时,求A,B两点间距离.
(3)在(2)的条件下,现A点静止不动,B点沿数轴向左运动时,经过多长时间A,B两点相距4个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A,B分别为数轴上的两点,点A表示的数是﹣30,点B表示的数是50.
![]()
(1)请写出线段AB中点M表示的数是 .
(2)现有一只蚂蚁P从点B出发,以每秒3个单位长度的速度沿数轴向左移动,同时另一只蚂蚁Q恰好从点A出发,以每秒2个单位长度的速度沿数轴向右移动,设两只蚂蚁在数轴上的点C相遇.
①求A、B两点间的距离;
②求两只蚂蚁在数轴上的点C相遇时所用的时间;
③求点C对应的数是多少?
(3)若蚂蚁P从点B出发,以每秒3个单位长度的速度沿数轴向左运动,同时另一只蚂蚁恰好从A点出发,以每秒2个单位长度的速度沿数轴也向左运动,设两只蚂蚁在数轴上的D点相遇,求D点表示的数是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若干个工人装卸一批货物,每个工人的装卸速度相同,如果这些工人同时工作,则需10小时装卸完毕;现改变装卸方式,开始一个人干,以后每隔t(整数)小时增加一个人干,每个参加装卸的人都一直干到装卸完毕,且最后参加的一个人装卸的时间是第一个人的![]() ,则按改变的方式装卸,自始至终共需时间_____小时.
,则按改变的方式装卸,自始至终共需时间_____小时.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+3(a≠0)经过点A(﹣1,0),B(![]() ,0),且与y轴相交于点C.
,0),且与y轴相交于点C.
(1)求这条抛物线的表达式;
(2)求∠ACB的度数;
(3)设点D是所求抛物线第一象限上一点,且在对称轴的右侧,点E在线段AC上,且DE⊥AC,当△DCE与△AOC相似时,求点D的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是由一些大小相同的小正方体组合成的简单几何体,并放在墙角.(注:图3、图4、图5每一个小方格的边长为1cm)
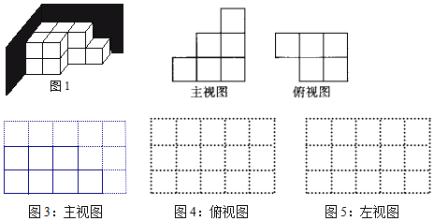
(1)该几何体主视图如图3所示,请在图4方格纸中画出它的俯视图;
(2)若将其露在外面的表面涂一层漆,则其涂漆面积为 cm2.(正方体的棱长为1cm)
(3)用一些小立方块搭一个几何体,使它的主视图和俯视图如图所示,它最少需要多少个小立方块?最多需要多少个小立方块?并在图5方格纸中画出需要最多小立方块的几何体的左视图.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com