
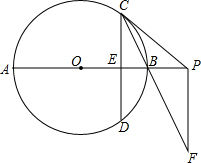
 如图,已知AB是⊙O的直径,弦CD⊥AB于E,过C点的切线交AB的延长线于P,过P点作PF∥CD交CB的延长线于F.
如图,已知AB是⊙O的直径,弦CD⊥AB于E,过C点的切线交AB的延长线于P,过P点作PF∥CD交CB的延长线于F.分析 (1)连接AC,OC,由PC是⊙O的切线,得到∠PCO=90°,于是得到∠PCF=90°-∠OCB,由于OC=OB,于是得到∠OCB=∠OBC=∠PBF,根据PF∥CD得到∠FPB=90°,于是得到∠F=∠PCB,即可得到结论;
(2)设半径为r,则有PB=5-r,由(1)知:PC=PF,在直角三角形PBF和直角三角形OCP中根据勾股定理得到PB2=FB2-PF2=FB2-PC2,PC2=PO2-OC2=52-r2,得到方程(5-r)2=(2$\sqrt{5}$)2-(52-r2)求得r=3,通过△ABC∽△FBP,得到比例式即可得到结果.
解答 (1)证明:连接AC,OC,
∵PC是⊙O的切线,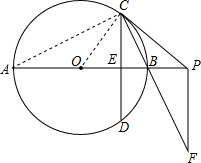
∴∠PCO=90°,
∴∠PCF=90°-∠OCB,
∵OC=OB,
∴∠OCB=∠OBC=∠PBF,
∵PF∥CD,
∴∠FPB=90°,
∴∠F=90°-∠PBF=90°-∠OCB,
∴∠F=∠PCB,
∴PC=PF;
(2)解:设半径为r,则有PB=5-r,
由(1)知:PC=PF,
∵∠FPB=90°,
∴PB2=FB2-PF2=FB2-PC2,
∵PC2=PO2-OC2=52-r2,
∴(5-r)2=(2$\sqrt{5}$)2-(52-r2)
解得:r=3,
∵∠ACB=∠BPF=90°,∠ABC=∠FBP,
∴△ABC∽△FBP,
∴$\frac{AB}{FB}=\frac{CB}{PB}$,即$\frac{6}{2\sqrt{5}}=\frac{BC}{5-3}$,
解得;CB=$\frac{6\sqrt{5}}{5}$.
点评 本题考查了切线的性质,勾股定理,相似三角形的判定和性质,等腰三角形的判定和性质,正确的作出辅助线是解题的关键.


 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次10公里的“迷你马拉松”训练中两人分别跑的路程y(公里)与时间x(分钟)的函数关系图象,他们同时出发,乙在75分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是$\frac{1}{6}$公里/分;(2)乙在冲刺阶段的速度$\frac{1}{5}$公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )
横店国际马拉松将于2015年5月17日鸣枪开跑,这个赛事的举办掀起了当地跑马拉松的热潮,如图是甲、乙两位马拉松爱好者在一次10公里的“迷你马拉松”训练中两人分别跑的路程y(公里)与时间x(分钟)的函数关系图象,他们同时出发,乙在75分钟的时候到达终点,并在终点等候甲,在甲跑完这个“迷你马拉松”的过程中,(1)甲前半程的速度是$\frac{1}{6}$公里/分;(2)乙在冲刺阶段的速度$\frac{1}{5}$公里/分;(3)在前半程甲一直领先于乙;(4)甲与乙刚好相距0.1公里的次数是4次.以上说法正确的个数是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,直线m∥n,将含有45°角的三角板ABC的一个锐角顶点C放在直线n上,则∠1+∠2等于( )
如图,直线m∥n,将含有45°角的三角板ABC的一个锐角顶点C放在直线n上,则∠1+∠2等于( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
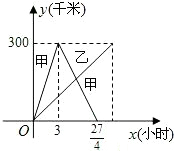 已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.
已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,2014个正方形按由小到大叠在一起,从大到小相间画出阴影,最外面的正方形的边长为2014cm,向里依次为2013cm,2012cm,…,1cm,那么在这个图形中,所有画阴影的面积和是多少?
如图,2014个正方形按由小到大叠在一起,从大到小相间画出阴影,最外面的正方形的边长为2014cm,向里依次为2013cm,2012cm,…,1cm,那么在这个图形中,所有画阴影的面积和是多少?查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )
如图,在地面上的点A处测得树顶B的仰角α=75°,若AC=6米,则树高BC为( )| A. | 6sin75°米 | B. | $\frac{6}{cos75°}$米 | C. | $\frac{6}{tan75°}$米 | D. | 6tan75°米 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com