
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖŌŚRt”÷ABCÖŠ£¬”ĻABC=90”ć£¬AB=6£¬BC=8£¬¶ÆµćMŅŌĆæĆė2øöµ„Ī»µÄĖŁ¶Č“ÓµćA³ö·¢£¬ŃŲ×ÅA”śB”śCµÄ·½ĻņŌĖ¶Æ£¬µ±µćMµ½“ļµćCŹ±£¬ŌĖ¶ÆĶ£Ö¹£®µćNŹĒµćM¹ŲÓŚµćBµÄ¶Ō³Ęµć£¬¹żµćM×÷MQ”ĶACÓŚµćQ£¬ŅŌMN£¬MQĪŖ±ß×÷MNPQ£¬ÉčµćMµÄŌĖ¶ÆŹ±¼äĪŖtĆė£®
£Ø1£©·Ö±šĒóµ±t=2ŗĶt=5Ź±£¬Ļ߶ĪMNµÄ³¤£»
£Ø2£©ŹĒ·ń“ęŌŚÕāŃłµÄtµÄÖµ£¬Ź¹µĆMNPQĪŖĮāŠĪ£æČō“ęŌŚ£¬ĒėĒó³ötµÄÖµ£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£»
£Ø3£©×÷µćP¹ŲÓŚÖ±ĻßMQµÄ¶Ō³ĘµćP'£¬µ±µćP'ĀäŌŚ”÷ABCÄŚ²æŹ±£¬ĒėÖ±½ÓŠ“³ötµÄȔֵ·¶Ī§£®
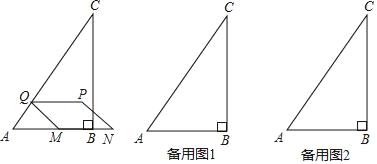
”¾“š°ø”æ£Ø1£©8£Ø2£©µ±t=![]() »ņ
»ņ![]() Ź±£¬ĖıߊĪMNPQĪŖĮāŠĪ£Ø3£©2£¼t£¼3»ņ3£¼t£¼
Ź±£¬ĖıߊĪMNPQĪŖĮāŠĪ£Ø3£©2£¼t£¼3»ņ3£¼t£¼![]() Ź±£¬µ±µćP'ĀäŌŚ”÷ABCÄŚ²æ
Ź±£¬µ±µćP'ĀäŌŚ”÷ABCÄŚ²æ
”¾½āĪö”æ
£Ø1£©t=2Ź±£¬µćMŌŚĻ߶ĪABÉĻ£¬Ēó³öAM¼“æÉ£¬t=5Ź±£¬µćMŌŚĻ߶ĪBCÉĻ£¬Ēó³öBM¼“æɽā¾öĪŹĢā£»
£Ø2£©·ÖĮ½ÖÖĒéŠĪ£¬·Ö±šĄūÓĆĻąĖĘČż½ĒŠĪµÄŠŌÖŹ¹¹½Ø·½³Ģ¼“æɽā¾öĪŹĢā£»
£Ø3£©·ÖĮ½ÖÖĒéŠĪ£ŗ¢ŁČēĶ¼3ÖŠ£¬µ±µćP¹ŲÓŚQMµÄ¶Ō³ĘµćP”äĀäŌŚĻ߶ĪABÉĻŹ±£®¢ŚČēĶ¼4ÖŠ£¬µ±µćPµÄ¶Ō³ĘµćĀäŌŚĻ߶ĪBCÉĻŹ±£¬·Ö±šĒó³ötµÄÖµ¼“æɽā¾öĪŹĢā.
£Ø1£©ÓÉĢāŅāµĆt=2£¬AM=4£¬MB=2£¬
”ßM”¢N¹ŲÓŚµćB¶Ō³Ę£¬
”ąBM=BN£¬
”ąMN=2BM=4
t=5£¬AB+BM=10£¬AB=6£¬MB=4£¬
”ąMN=2BM=8£®
£Ø2£©ĒéæöŅ»£ŗµ±µćMŌŚ±ßABÉĻŹ±£¬ČēĶ¼1£¬
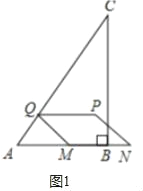
ÓÉ”÷AQM”×”÷ABC£¬æɵĆ![]() =
=![]() £¬
£¬
”ßAM=2t£¬AB=6£¬BC=8£¬AC=10£®
”ąQM=![]() t£¬BM=6©2t£¬MN=12©4t£®
t£¬BM=6©2t£¬MN=12©4t£®
QM=MNŹ±£¬¼“![]() t=12©4t£¬
t=12©4t£¬
½āµĆt=![]() £»
£»
Ēéæö¶ž£ŗµ±µćMŌŚ±ßBCÉĻŹ±£¬ČēĶ¼2£¬
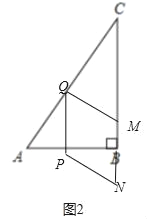
”÷CMQ”×”÷CAB£¬
”ą![]() £¬
£¬
”ą![]() £¬
£¬
”ąMQ=![]() £Ø14©2t£©£¬
£Ø14©2t£©£¬
”ßMN=MQ£¬
”ą2£Ø2t©6£©=![]() £Ø14©2t£©£¬
£Ø14©2t£©£¬
½āµĆ£ŗt=![]()
×ŪÉĻ£¬µ±t=![]() »ņ
»ņ![]() Ź±£¬ĖıߊĪMNPQĪŖĮāŠĪ£®
Ź±£¬ĖıߊĪMNPQĪŖĮāŠĪ£®
£Ø3£©ČēĶ¼3ÖŠ£¬
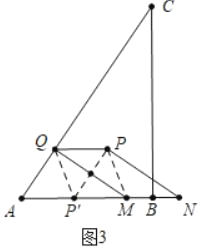
µ±µćP¹ŲÓŚQMµÄ¶Ō³ĘµćP”äĀäŌŚĻ߶ĪABÉĻŹ±£¬Ņ×Ö¤ĖıߊĪPQP”äMŹĒĮāŠĪ£¬
”ąPP”ä”ĶMQ£¬”ßMQ”ĶAC£¬
”ąPP”ä”ĪAC£¬”ßPQ”ĪAP”ä
”ąĖıߊĪAQPP”äŹĒĘ½ŠŠĖıߊĪ£¬
”ąAP”ä=PQ=MP”ä=MN£¬
”ąAM=2MN£¬
”ą2t=2£Ø6©2t£©
”ąt=2£¬
”ą
ČēĶ¼4£¬
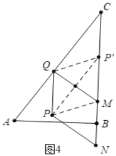
µ±µćPµÄ¶Ō³ĘµćĀäŌŚĻ߶ĪBCÉĻŹ±£¬Ņ×Ö¤ĖıߊĪPQP”äMŹĒĮāŠĪ£¬
æɵĆP”äM=P”äQ=CP”ä=MN£¬
”ąBM+CM=8£¬
”ą2t©6+2£Ø4t©12£©=8£¬
½āµĆt=![]() £¬
£¬
”ą3£¼t£¼![]() Ź±£¬µ±µćP'ĀäŌŚ”÷ABCÄŚ²æ£®
Ź±£¬µ±µćP'ĀäŌŚ”÷ABCÄŚ²æ£®
×ŪÉĻĖłŹö£¬2£¼t£¼3»ņ3£¼t£¼![]() Ź±£¬µ±µćP'ĀäŌŚ”÷ABCÄŚ²æ£®
Ź±£¬µ±µćP'ĀäŌŚ”÷ABCÄŚ²æ£®


 ÄÜĮ¦ĘĄ¼ŪĻµĮŠ“š°ø
ÄÜĮ¦ĘĄ¼ŪĻµĮŠ“š°ø ĢĘÓ”ĪÄ»ÆæĪŹ±²āĘĄĻµĮŠ“š°ø
ĢĘÓ”ĪÄ»ÆæĪŹ±²āĘĄĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖ¹żµćB£Ø1£¬0£©µÄÖ±Ļßl1ÓėÖ±Ļßl2£ŗy£½2x+4Ļą½»ÓŚµćP£Ø©1£¬a£©£¬l1ÓėyÖį½»ÓŚµćC£¬l2ÓėxÖį½»ÓŚµćA£®

£Ø1£©ĒóaµÄÖµ¼°Ö±Ļßl1µÄ½āĪöŹ½£®
£Ø2£©ĒóĖıߊĪPAOCµÄĆ껿£®
£Ø3£©ŌŚxÖįÉĻ·½ÓŠŅ»¶ÆÖ±ĻßĘ½ŠŠÓŚxÖį£¬·Ö±šÓėl1£¬l2½»ÓŚµćM£¬N£¬ĒŅµćMŌŚµćNµÄÓŅ²ą£¬xÖįÉĻŹĒ·ń“ęŌŚµćQ£¬Ź¹”÷MNQĪŖµČŃüÖ±½ĒČż½ĒŠĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öĀś×ćĢõ¼žµÄµćQµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æĪŖĮĖĀ䏵µ³µÄ”°¾«×¼·öʶ”±Õž²ß£¬A”¢BĮ½³Ē¾ö¶ØĻņC”¢DĮ½ĻēŌĖĖĶ·ŹĮĻŅŌÖ§³ÖÅ©“åÉś²ś£¬ŅŃÖŖA”¢BĮ½³Ē¹²ÓŠ·ŹĮĻ500¶Ö£¬ĘäÖŠA³Ē·ŹĮĻ±ČB³ĒÉŁ100¶Ö£¬“ÓA³ĒĶłC”¢DĮ½ĻēŌĖ·ŹĮĻµÄ·ŃÓĆ·Ö±šĪŖ20ŌŖ/¶ÖŗĶ25ŌŖ/¶Ö£»“ÓB³ĒĶłC”¢DĮ½ĻēŌĖ·ŹĮĻµÄ·ŃÓĆ·Ö±šĪŖ15ŌŖ/¶ÖŗĶ24ŌŖ/¶Ö£®ĻÖCĻēŠčŅŖ·ŹĮĻ240¶Ö£¬DĻēŠčŅŖ·ŹĮĻ260¶Ö£®
£Ø1£©A³ĒŗĶB³Ēø÷ÓŠ¶ąÉŁ¶Ö·ŹĮĻ£æ
£Ø2£©Éč“ÓA³ĒŌĖĶłCĻē·ŹĮĻx¶Ö£¬×ÜŌĖ·ŃĪŖyŌŖ£¬Ēó³ö×īÉŁ×ÜŌĖ·Ń£®
£Ø3£©ÓÉÓŚøü»»³µŠĶ£¬Ź¹A³ĒŌĖĶłCĻēµÄŌĖ·ŃĆæ¶Ö¼õÉŁa£Ø0£¼a£¼6£©ŌŖ£¬ÕāŹ±ŌõŃłµ÷ŌĖ²ÅÄÜŹ¹×ÜŌĖ·Ń×īÉŁ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ÓŠŅ»øöĮĄŅĀ¼Ü·ÅÖĆŌŚĖ®Ę½µŲĆęÉĻ£¬ŌŚĘäŹ¾ŅāĶ¼ÖŠ£¬Ö§¼ÜOA”¢OBµÄ³¤¾łĪŖ100cm£¬Ö§¼ÜOAÓėĖ®Ę½ĮĄŅĀ¼ÜOCµÄ¼Š½Ē”ĻAOCĪŖ59”ć£¬ŌņÖ§¼ÜĮ½øö×ŵŲµćÖ®¼äµÄ¾ąĄėABĪŖ_____cm£®
£Ø²Īæ¼Źż¾Ż£ŗsin59”ć”Ö0.86£¬cos59”ć”Ö0.52£¬tan59”ć”Ö1.66£©

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æij·ž×°µźÓĆ 6000 ŌŖ¹ŗ½ųŅ»Åś³ÄÉĄ£¬ŅŌ 60 ŌŖ/¼žµÄ¼Ūøń³öŹŪ£¬ŗÜæģŹŪĶź£¬Č»ŗóÓÖÓĆ 13500ŌŖ¹ŗ½ųĶ¬æī³ÄÉĄ£¬¹ŗ½ųŹżĮæŹĒµŚŅ»“ĪµÄ 2 ±¶£¬¹ŗ½ųµÄµ„¼Ū±ČÉĻŅ»“ĪĆ漞¶ą 5 ŌŖ£¬·ž×°µź ČŌ°“ŌŹŪ¼Ū 60 ŌŖ/¼ž³öŹŪ£¬²¢ĒŅČ«²æŹŪĶź.
£Ø1£©øĆ·ž×°µźµŚŅ»“Ī¹ŗ½ų³ÄÉĄ¶ąÉŁ¼ž£æ
£Ø2£©½«øĆ·ž×°µźĮ½“Ī¹ŗ½ų³ÄÉĄæ“×÷Ņ»±ŹÉśŅā£¬ÄĒĆ“Õā±ŹÉśŅāŹĒÓÆĄū»¹ŹĒæ÷Ėš£æĒó³öÓÆĄū£Ø»ņ æ÷Ėš£©¶ąÉŁŌŖ£æ
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
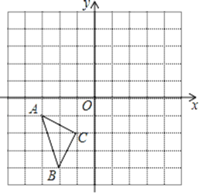
”¾ĢāÄæ”æŌŚČēĶ¼ĖłŹ¾µÄÖ±½Ē×ų±źĻµÖŠ£¬ĆæøöŠ”·½øń¶¼ŹĒ±ß³¤ĪŖ1µÄÕż·½ŠĪ£¬”÷ABCµÄ¶„µć¾łŌŚøńµćÉĻ£¬µćAµÄ×ų±źŹĒ(©3£¬©1)£®
£Ø1£©½«”÷ABCŃŲyÖįÕż·½ĻņĘ½ŅĘ3øöµ„Ī»µĆµ½”÷A1B1C1£¬»³ö”÷A1B1C1£¬²¢Š“³öµćB1µÄ×ų±ź£»
£Ø2£©»³ö”÷A1B1C1¹ŲÓŚyÖį¶Ō³ĘµÄ”÷A2B2C2£¬²¢Š“³öµćC2µÄ×ų±ź£»
£Ø3£©Ēó”÷ABCµÄĆ껿£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚ½ńÄźĪŅŹŠ³õ֊ѧŅµĖ®Ę½æ¼ŹŌĢåӿѧæʵÄÅ®×Ó800Ć×ÄĶĮ¦²āŹŌÖŠ£¬Ä³æ¼µćĶ¬Ź±ĘšÅܵĊ”ÓØŗĶŠ”Ć·ĖłÅܵÄĀ·³ĢS£ØĆ×£©ÓėĖłÓĆŹ±¼ät£ØĆė£©Ö®¼äµÄŗÆŹżĶ¼Ļó·Ö±šĪŖĻ߶ĪOAŗĶÕŪĻßOBCD£¬ĻĀĮŠĖµ·ØÕżČ·µÄŹĒ£Ø””””£©
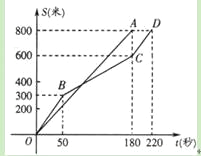
A”¢Š”ÓصÄĖŁ¶ČĖꏱ¼äµÄŌö“ó¶ųŌö“óB”¢Š”Ć·µÄĘ½¾łĖŁ¶Č±ČŠ”ÓصÄĘ½¾łĖŁ¶Č“ó
C”¢ŌŚĘšÅÜŗó180ĆėŹ±£¬Į½ČĖĻąÓöD”¢ŌŚĘšÅÜŗó50ĆėŹ±£¬Š”Ć·ŌŚŠ”ÓصÄĒ°Ćę
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
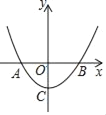
”¾ĢāÄæ”æČēĶ¼£¬¶ž“ĪŗÆŹży=x2©m2£Øm£¾0ĒŅĪŖ³£Źż£©µÄĶ¼ĻóÓėxÖį½»ÓŚµćA”¢B£ØAŌŚB×ó²ą£©£¬ÓėyÖį½»ÓŚC£®
£Ø1£©ĒóA£¬B£¬CČżµćµÄ×ų±ź£ØÓĆŗ¬mµÄŹ½×Ó±ķŹ¾£©£»
£Ø2£©Čō”ĻACB=90”ć£¬ĒómµÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖµćA£Ø12£¬0£©£¬OĪŖ×ų±źŌµć£¬PŹĒĻ߶ĪOAÉĻČĪŅ»µć£Ø²»ŗ¬¶ĖµćO”¢A£©£¬¶ž“ĪŗÆŹży1µÄĶ¼Ļó¹żP”¢OĮ½µć£¬¶ž“ĪŗÆŹży2µÄĶ¼Ļó¹żP”¢AĮ½µć£¬ĖüĆĒµÄæŖæŚ¾łĻņĻĀ£¬¶„µć·Ö±šĪŖB”¢C£¬ÉäĻßOBÓėÉäĻßACĻą½»ÓŚµćD£®Ōņµ±OD=AD=9Ź±£¬ÕāĮ½øö¶ž“ĪŗÆŹżµÄ×ī“óÖµÖ®ŗĶµČÓŚ£Ø””””£©
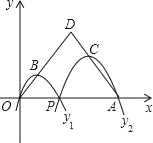
A. 8 B. 3![]() C. 2
C. 2![]() D. 6
D. 6
²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com