
【题目】如图,在△ABC中,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC ;
(2)若∠BAC=![]() ,试判断四边形ADCF的形状,并证明你的结论.
,试判断四边形ADCF的形状,并证明你的结论.

 名师点拨卷系列答案
名师点拨卷系列答案科目:初中数学 来源: 题型:
【题目】图1所示矩形ABCD中,BC=x,CD=y,y与x满足的反比例函数关系如图2所示,等腰直角三角形AEF的斜边EF过C点,M为EF的中点,则下列结论正确的是
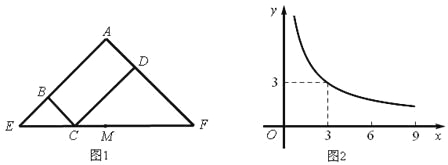
A. 当x=3时,EC<EM B. 当y=9时,EC>EM
C. 当x增大时,EC·CF的值增大。 D. 当y增大时,BE·DF的值不变。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(如图平面直角坐标系内,已知点A的坐标是(-3,0).
(1)点B的坐标为_______,点C的坐标为_____,∠BAC=______;
(2)求△ABC的面积;
(3)点P是y轴负半轴上的一个动点,连接BP交![]() 轴于点D,是否存在点P使得
轴于点D,是否存在点P使得
△ADP与△BC的面积相等?若存在,请直接写出点P的坐标;若不存在,请说明理由.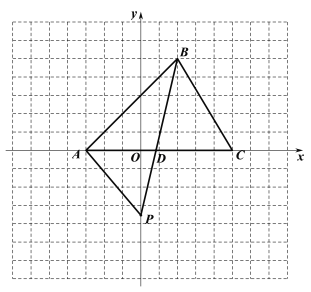
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() .试说明
.试说明![]() ∥
∥![]() ,请完成下列填空,把证明过程补充完整.
,请完成下列填空,把证明过程补充完整.
证明: ∵ __________________________ ,
∴ ![]() (_________________).
(_________________).
∴![]()
又∵![]()
∴ __________________ (_____________________),
∴![]() ∥
∥![]() (_______________________________).
(_______________________________).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读求绝对值不等式![]() 和
和![]() 的解集过程:
的解集过程:
对于绝对值不等式![]() ,从图1所示的数轴上看:大于
,从图1所示的数轴上看:大于![]() 而小于
而小于![]() 的数绝对值是小于
的数绝对值是小于![]() 的,所以
的,所以![]() 的解集是
的解集是![]() ;
;
对于绝对值不等式![]() ,从图2所示的数轴上看:小于
,从图2所示的数轴上看:小于![]() 而大于
而大于![]() 的数绝对值是大于
的数绝对值是大于![]() 的,所以
的,所以![]() 的解集…….
的解集…….


解答下面的问题:
解不等式:⑴.![]() ; ⑵.
; ⑵.![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】去年春季,蔬菜种植场在15公顷的大棚地里分别种植了茄子和西红柿,总费用是![]() 万元
万元![]() 其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
其中,种植茄子和西红柿每公顷的费用和每公顷获利情况如表:
每公顷费用 | 每公顷获利 | |
茄子 |
|
|
西红柿 |
|
|
请解答下列问题:
![]() 求出茄子和西红柿的种植面积各为多少公顷?
求出茄子和西红柿的种植面积各为多少公顷?
![]() 种植场在这一季共获利多少万元?
种植场在这一季共获利多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com