
【题目】如图,AB是![]() O的直径,AB=4,C为
O的直径,AB=4,C为![]() 的三等分点(更靠近A点),点P是
的三等分点(更靠近A点),点P是![]() O上一个动点,取弦AP的中点D,则线段CD的最大值为( )
O上一个动点,取弦AP的中点D,则线段CD的最大值为( )

A.2B.![]() C.
C.![]() D.
D.![]()
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在锐角三角形ABC中,点D,E分别在边AC,AB上,AG⊥BC于点G,AF⊥DE于点F,∠EAF=∠GAC.
(1)求证:△ADE∽△ABC;
(2)若AD=3,AB=5,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
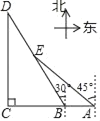
【题目】如图为某景区五个景点A,B,C,D,E的平面示意图,B,A在C的正东方向,D在C的正北方向,D,E在B的北偏西30°方向上,E在A的西北方向上,C,D相距1000![]() m,E在BD的中点处.
m,E在BD的中点处.
(1)求景点B,E之间的距离;
(2)求景点B,A之间的距离.(结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某蔬菜加工公司先后两批次收购洋葱共100吨.第一批洋葱价格为4000元/吨;因洋葱大量上市,第二批价格跌至1000元/吨.这两批洋葱共用去16万元.
(1)求两批次购进洋葱各多少吨;
(2)公司收购后对洋葱进行加工,分为粗加工和精加工两种:粗加工每吨利润400元,精加工每吨利润1000元.要求精加工数量不多于粗加工数量的三倍.为获得最大利润,精加工数量应为多少吨?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形ABCD的顶点A点,D点分别在x轴、y轴上,对角线BD∥x轴,反比例函数![]() 的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )
的图象经过矩形对角线的交点E,若点A(2,0),D(0,4),则k的值为( )
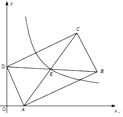
A.16B.20C.32D.40
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点M是边BC上的一点(不与B、C重合),点N在CD边的延长线上,且满足∠MAN=90°,联结MN、AC,MN与边AD交于点E.
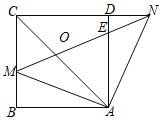
(1)求证:AM=AN;
(2)如果∠CAD=2∠NAD,求证:AM2=ACAE;
(3)MN和AC相交于O点,若BM=1,AB=3,试猜想线段OM,ON的数量关系并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线x=t(t>0)与双曲线y=![]() (k1>0)交于点A,与双曲线y=
(k1>0)交于点A,与双曲线y=![]() (k2<0)交于点B,连接OA,OB.
(k2<0)交于点B,连接OA,OB.
(1)当k1、k2分别为某一确定值时,随t值的增大,△AOB的面积_______(填增大、不变、或减小)
(2)当k1+k2=0,S△AOB=8时,求k1、k2的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com