
【题目】我市中小学全面开展“阳光体育”活动,某校在大课间中开设了A:体操,B:跑操,C:舞蹈,D:健美操四项活动,为了解学生最喜欢哪一项活动,随机抽取了部分学生进行调查,并将调查结果绘制成了如下两幅不完整的统计图,请根据统计图回答下列问题: 
(1)这次被调查的学生共有人.
(2)请将统计图2补充完整.
(3)统计图1中B项目对应的扇形的圆心角是度.
(4)已知该校共有学生3600人,请根据调查结果估计该校喜欢健美操的学生人数.
【答案】
(1)500
(2)解:A的人数:500﹣75﹣140﹣245=40(人);
补全条形图如图:

(3)54
(4)解:245÷500×100%=49%,
3600×49%=1764(人)
【解析】解:(1)140÷28%=500(人), 故答案为:500; (3)75÷500×100%=15%,
360°×15%=54°,
故答案为:54;
(1)利用C的人数÷所占百分比可得被调查的学生总数;(2)利用总人数减去其它各项的人数=A的人数,再补图即可;(3)计算出B所占百分比,再用360°×B所占百分比可得答案;(4)首先计算出样本中喜欢健美操的学生所占百分比,再利用样本估计总体的方法计算即可.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
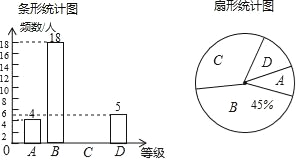
【题目】“足球运球”是中考体育必考项目之一.兰州市某学校为了解今年九年级学生足球运球的掌握情况,随机抽取部分九年级学生足球运球的测试成绩作为一个样本,按A,B,C,D四个等级进行统计,制成了如下不完整的统计图.(说明:A级:8分﹣10分,B级:7分﹣7.9分,C级:6分﹣6.9分,D级:1分﹣5.9分)
根据所给信息,解答以下问题:
(1)在扇形统计图中,C对应的扇形的圆心角是 度;
(2)补全条形统计图;
(3)所抽取学生的足球运球测试成绩的中位数会落在 等级;
(4)该校九年级有300名学生,请估计足球运球测试成绩达到A级的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一种商品,单价30元,试销中发现这种商品每天的销售量夕(件)与每件的销售价![]() (元)满足关系:
(元)满足关系:![]() =100-2
=100-2![]() .若商店每天销售这种商品要获得200元的销售利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
.若商店每天销售这种商品要获得200元的销售利润,那么每件商品的售价应定为多少元?每天要售出这种商品多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知五边形OABCD的顶点O在坐标原点,点A在y轴上,点D在x轴上,AB∥x轴,CD∥y轴,动点P从点O出发,以每秒1单位的速度,沿五边形OABCD的边顺时针运动一周,顺次连结P,O,A三点所围成图形的面积为S,点P的运动时间为t秒,S与t之间的函数关系如图2中折线OEFGHI所示.
(1)求证:AB=2;
(2)求五边形OABCD的面积.
(3)求直线BC的函数表达式;
(4)若直线OP把五边形OABCD的面积分成1:3两部分,求点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校开展“文明礼仪”演讲比赛,八(1)班、八(2)班派出的5名选手的比赛成绩如图所示.
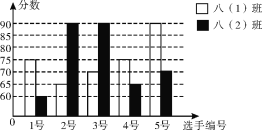
(1)根据上图,完成表格.
平均数 | 中位数 | 方差 | |
八(1)班 | 75 | _______ | _______ |
八(2)班 | 75 | 70 | 160 |
(2)结合两班选手成绩的平均数和方差,分析两个班级参加比赛的选手的成绩.
(3)如果在每班参加比赛的选手中分别选出3人参加决赛,从平均分看,你认为哪个班的实力更强一些?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,若点P(x,y)的坐标x、y均为整数,则称点P为格点,若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L,例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.
(1)求出图中格点四边形DEFG对应的S,N,L的值.
(2)已知格点多边形的面积可表示为S=N+aL+b,其中a,b为常数,若某格点多边形对应的N=82,L=38,求S的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一副三角板按如图所示叠放在一起,若固定![]() ,将
,将![]() 绕着公共顶点
绕着公共顶点![]() ,按顺时针方向旋转
,按顺时针方向旋转![]() 度
度![]() ,当
,当![]() 的一边与
的一边与![]() 的某一边平行时,相应的旋转角
的某一边平行时,相应的旋转角![]() 的度数为_________________。
的度数为_________________。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程m(x+h)2+k=0(m,h,k均为常数,m≠0)的解是x1=﹣3,x2=2,则方程m(x+h﹣3)2+k=0的解是( )
A.x1=﹣6,x2=﹣1
B.x1=0,x2=5
C.x1=﹣3,x2=5
D.x1=﹣6,x2=2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在数轴上有A,B两点,点A表示的数为4,点B在A点的左边,且AB=12.若有一动点P从数轴上点A出发,以每秒1个单位长度的速度沿数轴向左匀速运动,动点Q从点B出发,以每秒2个单位长度的速度沿着数轴向右匀速运动,设运动时间为t秒.
![]()
(1)写出数轴上点B表示的数为________,P所表示的数为________(用含t的代数式表示);
(2)若点P,Q分别从A,B两点同时出发,问点P运动多少秒与Q相距3个单位长度?
(3)若点P,Q分别从A,B两点同时出发,分别以BQ和AP为边,在数轴上方作正方形BQCD和正方形APEF如图所示.求当t为何值时,两个正方形的重叠部分面积是正方形APEF面积的一半?请直接写出结论:t=__________秒.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com