26、阅读：
我们约定，若一个三角形（记为△M
1）是由另一个三角形（记为△M）通过一次平移得到的，称为△M经过T变换得到△M
1，若一个三角形（记为△M
2）是由另一个三角形（记为△M）通过绕其任一边中点旋转180°得到的，称为△M经过R变换得到△M
2．以下所有操作中每一个三角形只可进行一次变换，且变换均是从图中的基本三角形△A开始的，通过变换形成的多边形中的任意两个小三角形（指与△A全等的三角形）之间既无缝隙也无重叠．
操作：
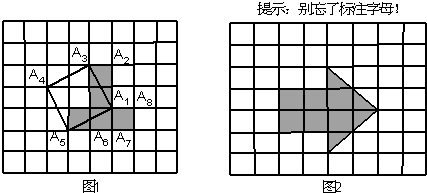
（1）如图，由△A经过R变换得到△A
1，又由△A
1经过
R
变换得到△A
2，再由△A
2经过
T
变换得到△A
3，形成了一个大三角形，记作△B．
（2）在下图的基础上继续变换下去得到△C，若△C的一条边上恰有3个基本三角形（指有一条边在该边上的基本三角形），则△C含有
9
个基本三角形；若△C的一条边上恰有11个基本三角形，则△C含有
121
个基本三角形；
应用：
（3）若△A是正三角形，你认为通过以上两种变换可以得到的正多边形是
正六边形，正三角形
；
（4）请你用两次R变换和一次T变换构成一个四边形，画出示意图，并仿照下图作出标记．
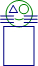下图中的图是由图平移得到的．
阅读快车系列答案
1、下图中的图（ ）是由图平移得到的．