【题目】已知：在四边形ABCD中，∠ABC=∠ADC=90，M、N分别是CD和BC上的点．
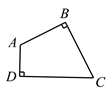
求作：点M、N，使△AMN的周长最小．
作法：如图，
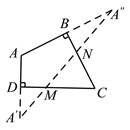
（1）延长AD，在AD的延长线上截取DA=DA；
（2）延长AB，在AB的延长线上截取B A″=BA；
（3）连接A′A″，分别交CD、BC于点M、N．则点M、N即为所求作的点．
请回答：这种作法的依据是_____________．
【答案】①线段垂直平分线的定义（或线段垂直平分线的判定，或轴对称的性质即对称点的连线段被对称轴垂直平分）
②线段垂直平分线上的点到线段两个端点的距离相等（线段垂直平分线的性质）；
③两点之间线段最短.
【解析】分析：分别作出点A关于CD，BC的对称点A′，A″，连接A′A″分别交CD、BC于点M、N此时△AMN周长最小．
详解：作图的依据是：①线段垂直平分线的定义（或线段垂直平分线的判定，或轴对称的性质即对称点的连线段被对称轴垂直平分）
②线段垂直平分线上的点到线段两个端点的距离相等（线段垂直平分线的性质）；
③两点之间线段最短．
故答案为：①线段垂直平分线的定义（或线段垂直平分线的判定，或轴对称的性质即对称点的连线段被对称轴垂直平分）
②线段垂直平分线上的点到线段两个端点的距离相等（线段垂直平分线的性质）；
③两点之间线段最短．
字词句段篇系列答案科目：初中数学 来源： 题型：
【题目】下列说法中，正确的是（ ）
A.直线外一点到这条直线的垂线段，叫做点到直线的距离；
B.已知线段
，
轴，若点
的坐标为（-1，2），则点
的坐标为（-1，-2）或（-1，6）；
C.若
与
互为相反数，则
；
D.已知关于
的不等式
的解集是
，则
的取值范围为
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，数轴的单位长度为1
（1）如果点
表示的数互为相反数，那么点
表示的数是_______，点
表示的数是_______；
（2）如果点
表示的数互为相反数，那么四点中，点_______表示的数的绝对值最大，请简要说明理由；
（3）当点为原点时，若存在一点
到点
的距离是点到点
的距离的2倍，则点所表示的数是_______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】小明从家出发到公园晨练，在公园锻炼一段时间后按原路返回，同时小明爸爸从公园按小明的路线返回家中．如图是两人离家的距离
（米）与小明出发的时间
（分）之间的关系，则小明出发______分钟后与爸爸相遇．
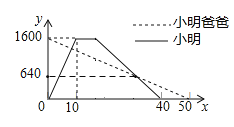
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】抛物线y=ax2+bx+3（a≠0）经过点A（﹣1，0），B（
，0），且与y轴相交于点C．
（1）求这条抛物线的表达式；
（2）求∠ACB的度数；
（3）设点D是所求抛物线第一象限上一点，且在对称轴的右侧，点E在线段AC上，且DE⊥AC，当△DCE与△AOC相似时，求点D的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】出租车司机小李某天下午运营全是在东西走向的人民大道上进行的，如果规定向东为正，向西为负，他这天下午行驶里程如下：（单位：千米）
+15, -3, +14，-11，+10，-12，+4，-15，+16，-18
（1）他将最后一名乘客送到目的地时，距下午出车地点是多少千米？
（2）若汽车耗油量为
升∕千米，这天下午共耗油多少升
查看答案和解析>>
科目：初中数学 来源： 题型：
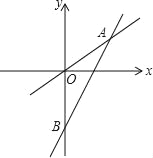
【题目】如图表示一个正比例函数与一个一次函数的图象，它们交于点A（4，3），一次函数的图象与y轴交于点B，且OA=OB．
（1）求这两个函数的解析式；
（2）求△OAB的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知AB∥CD，F为CD上一点，∠EFD=60°，∠AEC=2∠CEF，若6°＜∠BAE＜15°，∠C的度数为整数，则∠C的度数为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，⊙O的半径OD⊥弦AB于点C，连接BO并延长交⊙O于点E，连接AE，若AB=6，CD=1，则AE的长为（ ）
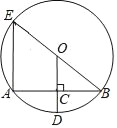
A. 3
B. 8 C. 12 D. 8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com