
| A. | 由-2y-5=-1+y,得-2y-y=5-1 | B. | 由-3x=-6,得x=2 | ||
| C. | 由$\frac{1}{5}$y=2,得y=10 | D. | 由-2(1-2x)+3=0,得-2+4x+3=0 |
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案 黄冈创优卷系列答案
黄冈创优卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
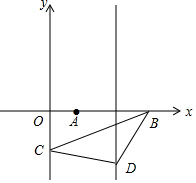 已知,二次函数y=ax2+bx-2的图象经过A(1,0)、B(4,0),且与y轴交于点C.
已知,二次函数y=ax2+bx-2的图象经过A(1,0)、B(4,0),且与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
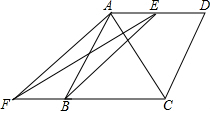 如图,在菱形ABCD中,E是AD的中点,EF⊥AC交CB的延长线于点F,连接AF,BE.
如图,在菱形ABCD中,E是AD的中点,EF⊥AC交CB的延长线于点F,连接AF,BE.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
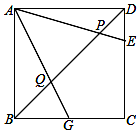 如图,点E、G分别是正方形ABCD的边CD、BC上的点,连接AE、AG分别交对角线BD于点P、Q.若∠EAG=45°,BQ=4,PD=3,则正方形ABCD的边长为( )
如图,点E、G分别是正方形ABCD的边CD、BC上的点,连接AE、AG分别交对角线BD于点P、Q.若∠EAG=45°,BQ=4,PD=3,则正方形ABCD的边长为( )| A. | 6$\sqrt{2}$ | B. | 7 | C. | 7$\sqrt{2}$ | D. | 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
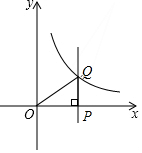 如图,点P是x轴正半轴上的一个动点,过点P作PQ⊥x轴交双曲线y=$\frac{1}{x}$(x>0)于点Q,连结OQ,当点P沿x轴的正方向运动时,Rt△QOP的面积( )
如图,点P是x轴正半轴上的一个动点,过点P作PQ⊥x轴交双曲线y=$\frac{1}{x}$(x>0)于点Q,连结OQ,当点P沿x轴的正方向运动时,Rt△QOP的面积( )| A. | 保持不变 | B. | 逐渐减少 | C. | 逐渐增大 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
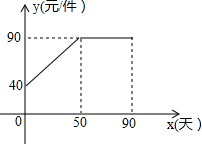 九年级(1)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售的相关信息如下,已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为W(单位:元)
九年级(1)班数学兴趣小组经过市场调查整理出某种商品在第x天(1≤x≤90,且x为整数)的售价与销售的相关信息如下,已知商品的进价为30元/件,设该商品的售价为y(单位:元/件),每天的销售量为p(单位:件),每天的销售利润为W(单位:元)| 时间x(天) | 1 | 30 | 60 | 90 |
| 每天销售量p(件) | 198 | 140 | 80 | 20 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com