
已知点E、F为抛物线![]() 上的两点,过点E、F分别作
上的两点,过点E、F分别作![]() 轴的垂线,分别交
轴的垂线,分别交![]() 轴于点B、D,交直线
轴于点B、D,交直线![]() 于点A、C,设S为直线AB、CD与
于点A、C,设S为直线AB、CD与![]() 轴、直线
轴、直线![]() 所围成图形的面积。
所围成图形的面积。
(1)当![]() ,
,![]() ,
,![]() 时,计算:①当
时,计算:①当![]() ,
,![]() 时,求
时,求![]() 、
、![]() 、S;②当
、S;②当![]() ,
,![]() 时,求
时,求![]() 、
、![]() 、S;通过以上的计算,猜想S与
、S;通过以上的计算,猜想S与![]() -
-![]() 的数量关系;
的数量关系;
(2)当抛物线![]() 在
在![]() 轴上方,且点
轴上方,且点![]() 、
、![]() 在抛物线
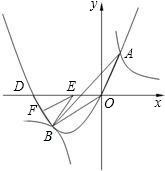
在抛物线![]() 的对称轴的同侧(点E在点F的左侧)时(如图1),(1)中的结论是否仍然成立?请说明你的判断;
的对称轴的同侧(点E在点F的左侧)时(如图1),(1)中的结论是否仍然成立?请说明你的判断;
(3)如果将(2)中的“同侧”改为“异侧”(如图2),其他条件不变,并设M为直线![]() 与
与![]() 轴交点,
轴交点,![]() ,
,![]() ,求
,求![]() 、
、![]() 与
与![]() 、
、![]() 的数量关系(直接写出答案)。
的数量关系(直接写出答案)。

 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案科目:初中数学 来源: 题型:
| k | x |
 的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).
的坐标为(1,4),点B在第三象限内,且△AOB的面积为3(O为坐标原点).查看答案和解析>>
科目:初中数学 来源: 题型:
 面直角坐标系.
面直角坐标系.查看答案和解析>>
科目:初中数学 来源: 题型:
 (2013•常熟市模拟)如图,抛物线y=ax2+bx(a>0)与双曲线y=
(2013•常熟市模拟)如图,抛物线y=ax2+bx(a>0)与双曲线y=| k |
| x |
| 2 |
| 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com