练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    如图所示，EA平分∠CAB，且AB＝AC＋BD，E为CD中点，求证：BE平分∠ABD．

    答案：
    解析：

    在AB上取AF＝AC


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

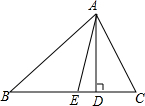    （1）如图所示，在△ABC中，AD丄BC于D，AE平分∠BAC，且∠C大于∠B，求证：∠EAD=
    1
    2
    （∠C-∠B）．
    （2）若把问题（1）中的“AD丄BC”改为“点F为EA上一点且FD丄BC于D”，画出新的图形，并试说明∠EFD=
    1
    2
    （∠C-∠B）．
    （3）若把问题（2）中的“F为EA上一点”改为“F为AE延长线上的一点”，则问题（2）中的结论成立吗？请说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源：非常讲解·教材全解全析　数学　九年级下　（配北师大课标） 配北师大课标 题型：044

    如图所示，已知△ABC中，∠BAC的平分线与边BC和外接圆分别相交于点D和E，延长AC交过D、E、C三点的圆于点F．

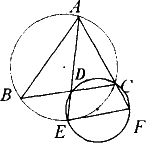
    (1)求证：EF2＝ED·EA；

    (2)若AE＝6，EF＝3，求AF·AC的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

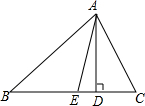    （1）如图所示，在△ABC中，AD丄BC于D，AE平分∠BAC，且∠C大于∠B，求证：∠EAD=数学公式（∠C-∠B）．
    （2）若把问题（1）中的“AD丄BC”改为“点F为EA上一点且FD丄BC于D”，画出新的图形，并试说明∠EFD=数学公式（∠C-∠B）．
    （3）若把问题（2）中的“F为EA上一点”改为“F为AE延长线上的一点”，则问题（2）中的结论成立吗？请说明你的理由．

    查看答案和解析>>

    科目：初中数学 来源：同步题 题型：解答题

    数学课堂上，徐老师出示了一道试题：如图所示，在正三角形ABC中M是BC边（不含端点B，C）上任意一点.P是BC延长线上一点，N是∠ACP的平分线上一点，若∠AMN=60°，求证：AM=MN。
    （1）经过思考，小明展示了一种正确的证明过程，请你将证明过程补充完整。证明：在AB上截取EA=MC，连接EM，得△AEM
    ∵∠1=180°-∠AMB-∠AMN，∠2=180°-∠AMB-∠B，∠AMN=∠B=60°，
    ∴∠1=∠2
    又∵CN平分∠ACP，
    ∴∠4=∠ACP=60°
    ∴∠MCN=∠3+∠4=120° ①
    又∵BA=BC，EA=MC，
    ∴BA-EA=BC-MC
    即：BE=BM
    ∴△BEM为等边三角形
    ∴∠6=60°
    ∴∠5=180°-6=120°。②
    由①②得∠MCN=∠5
    在△AEM和△MCN中
    ∴（         ），（           ），（         ），
    ∴△AEM≌△MCN（ASA）
    ∴AM=MN。
    （2）若将试题中的“正三角形ABC”改为“正方形A1B1C1D1”（如图），N1是∠D1C1P1的平分线上一点，则当∠A1M1N1=90°时，结论A1M1=M1N1是否还成立？
    （3）若将题中的“正三角形ABC”改为“正多边形AnBnCnDn…Xn”，请你猜想：当∠AnMnNn=（     ）时，结论AnMn=MnNn仍然成立？（直接写出答案，不需要证明）

    查看答案和解析>>

    同步练习册答案