
已知抛物线y=ax2-4ax+c经过点A(0,2),顶点B的纵坐标为3.将直线AB向下平移,与x轴、y轴分别交于点C、D,与抛物线的一个交点为P,若D是线段CP的中点,则点P的坐标为_________.
(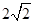 ,
,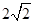 )
)
解析试题分析:首先求出顶点坐标,利用待定的系数法求得物线的解析式;求出直线AB,进一步得到直线PC的解析式,由此联立一元二次方程求得结果.
试题解析:抛物线y=ax2-4ax+b的对称轴是x=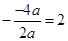 ,顶点坐标为B(2,3),且经过A(0,2),
,顶点坐标为B(2,3),且经过A(0,2),
代入函数解析式得 ,
,
解得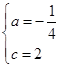 ,
,
所以函数解析式为y=?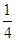 x2+x+2;
x2+x+2;
如图,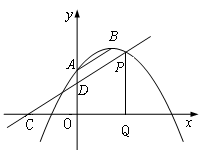
设P点坐标为(x,?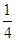 x2+x+2),过点P作PQ⊥x轴,垂足为Q,可得到△COD∽△CQP,
x2+x+2),过点P作PQ⊥x轴,垂足为Q,可得到△COD∽△CQP, ,又因为
,又因为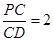 ,所以
,所以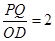
因此D点坐标为(0,?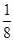 x2+
x2+ x+1),
x+1),
经过A、B两点直线AB的解析式为y= x+2,
x+2,
因此直线CP的解析式为y= x+(-
x+(-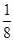 x2+
x2+ x+1)=-
x+1)=-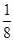 x2+x+1,与抛物线联立方程得,
x2+x+1,与抛物线联立方程得,
-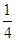 x2+x+2=-
x2+x+2=-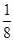 x2+x+1,解得x=
x2+x+1,解得x=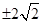 ,(负舍去)
,(负舍去)
代入抛物线解析式可得y=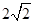 ,
,
因此P点坐标为P(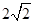 ,
,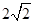 ).
).
考点: 二次函数综合题.


科目:初中数学 来源: 题型:填空题
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a-b=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确的是 ( ).(填正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
某服装店销售童装平均每天售出20件,每件赢利50元,根据销售经验:如果每件童装降价4元,那么平均每天就可以多售出4件。则每件童装应降价 元时,每天能获得最大利润。
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
(定义[a,b,c]为函数 的特征数,下面给出特征数为 [2m,1-m,-1-m]的函数的一些结论:
的特征数,下面给出特征数为 [2m,1-m,-1-m]的函数的一些结论:
①当m=-3时,函数图象的顶点坐标是( ,
, );
);
②当m>0时,函数图象截x轴所得的线段长度大于 ;
;
③当m<0时,函数在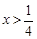 时,y随x的增大而减小;
时,y随x的增大而减小;
④当m≠0时,函数图象经过x轴上一个定点.
其中正确的结论有________ .(只需填写序号)
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
二次函数 (a≠0)中的自变量x与函数值y的部分对应值如下表:
(a≠0)中的自变量x与函数值y的部分对应值如下表:
| x | … | - | -1 | - | 0 | 1 | … | ||
| y | … | - | -2 | - | -2 | - | 0 | … |
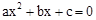 的解为 .
的解为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com