
 如图,把大小相等的两个长方形拼成L形图案,则∠FCA=45度.
如图,把大小相等的两个长方形拼成L形图案,则∠FCA=45度. 分析 根据题意可证△AEF≌△CDA,可得AF=AC,∠FAC=90°,从而得出△ACF为等腰直角三角形,进而得出答案.
解答 解:∵两个长方形的大小完全相同,
∴EF=DA,∠AEF=∠CDA=90°,EA=DC,
在△AEF和△CDA中
$\left\{\begin{array}{l}{EF=DA}\\{∠FEA=∠ADC}\\{AE=DC}\end{array}\right.$,
∴△AEF≌△CDA(SAS),
∴AF=AC,∠EAF=∠DCA,
又∵∠DCA+∠DAC=90°,
∴∠EAF+∠DAC=90°,
即∠FAC=90°,
∴△ACF为等腰直角三角形,
∴∠FCA=45°.
故答案为:45.
点评 本题考查了图形的剪拼、全等三角形的判定与性质、等腰直角三角形的判定,理解两个长方形的大小完全相同的含义是解题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
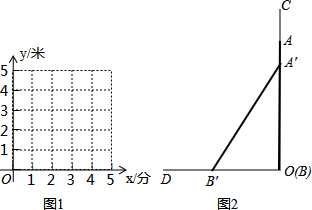
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 销售时段 | 销售数量 | 销售收入 | |
| A种型号 | B种型号 | ||
| 第一周 | 4台 | 5台 | 7100元 |
| 第二周 | 6台 | 10台 | 12600元 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,有一枚质地均匀的正十二面体形状的骰子,其中1个面标有“0”,1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,其余的面标有“5”,将这枚骰子掷出后:
如图,有一枚质地均匀的正十二面体形状的骰子,其中1个面标有“0”,1个面标有“1”,2个面标有“2”,3个面标有“3”,4个面标有“4”,其余的面标有“5”,将这枚骰子掷出后:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b-3)2=0.
如图,在平面直角坐标系中,已知A(a,0),B(b,0),其中a,b满足|a+1|+(b-3)2=0.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知如图,一天上午6点钟,言老师从学校出发,乘车上市里开会,8点准时到会场,中午12点钟回到学校,他这一段时间内的行程S(km)(即离开学校的距离)与时间(时)的关系可用图中的折线表示,根据图提供的有关信息,解答下列问题:
已知如图,一天上午6点钟,言老师从学校出发,乘车上市里开会,8点准时到会场,中午12点钟回到学校,他这一段时间内的行程S(km)(即离开学校的距离)与时间(时)的关系可用图中的折线表示,根据图提供的有关信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com