
 如图,AB为东西走向的一条公路,C是公路旁边的一个村子,现在准备从村庄C修一条公路CD到公路AB,在A点时测得村庄C在它的北偏东45°方向上,沿正东方向4千米后到达B处,此时村庄C在它的北偏西55°方向上,求公路CD的最短长度.(结果精确到0.1千米,参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.4281)
如图,AB为东西走向的一条公路,C是公路旁边的一个村子,现在准备从村庄C修一条公路CD到公路AB,在A点时测得村庄C在它的北偏东45°方向上,沿正东方向4千米后到达B处,此时村庄C在它的北偏西55°方向上,求公路CD的最短长度.(结果精确到0.1千米,参考数据:sin55°≈0.8192,cos55°≈0.5736,tan55°≈1.4281) 分析 如图作CD⊥AB于点D,此时CD最短,设CD=x,根据tan∠CBD=$\frac{CD}{DB}$,列出方程即可解决.
解答 解: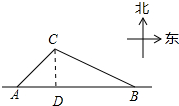 如图作CD⊥AB于点D,此时CD最短,设CD=x,
如图作CD⊥AB于点D,此时CD最短,设CD=x,
∵∠A=45°,∠ADC=∠BDC=90°,
∴∠ACD=∠A=45°,
∴CD=AD=x,
∵tan∠BCD=$\frac{BD}{CD}$,
∴tan55°=$\frac{4-x}{x}$,
∴1.4281=$\frac{4-x}{x}$,
∴x≈1.6.
∴CD的最小值为1.6千米.
点评 本题考查解直角三角形-方向角,三角函数,等腰直角三角形性质等知识,解题的关键是灵活应用三角函数,构建方程解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:选择题
| A. | 有最大值-1 | B. | 有最小值-1 | C. | 有最大值1 | D. | 有最小值1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
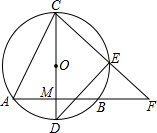 如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交AB的延长线于点F,连结DE.
如图,⊙O的弦AB=8,直径CD⊥AB于M,OM:MD=3:2,E是劣弧CB上一点,连结CE并延长交AB的延长线于点F,连结DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3.6 元 | B. | 5 元 | C. | 10 元 | D. | 12 元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 12 | B. | 10 | C. | 8 | D. | 9 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com