
【题目】若ab<0,则正比例函数y=ax与反比例函数 ![]() 在同一坐标系中的大致图象可能是( )
在同一坐标系中的大致图象可能是( )
A.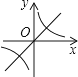
B.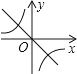
C.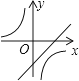
D.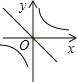
【答案】D
【解析】∵ab<0,∴分两种情况: ①当a>0,b<0时,正比例函数y=ax的图象过原点、第一、三象限,反比例函数图象在第二、四象限,无此选项;
②当a<0,b>0时,正比例函数的图象过原点、第二、四象限,反比例函数图象在第一、三象限,选项D符合.
故选:D.
【考点精析】根据题目的已知条件,利用正比例函数的图象和性质和反比例函数的图象的相关知识可以得到问题的答案,需要掌握正比函数图直线,经过一定过原点.K正一三负二四,变化趋势记心间.K正左低右边高,同大同小向爬山.K负左高右边低,一大另小下山峦;反比例函数的图像属于双曲线.反比例函数的图象既是轴对称图形又是中心对称图形.有两条对称轴:直线y=x和 y=-x.对称中心是:原点.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:
【题目】下列各式中:
①由3x=﹣4系数化为1得x=﹣![]() ;
;
②由5=2﹣x移项得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括号得4x﹣2﹣3x﹣9=1.
其中正确的个数有( )
A. 0个 B. 1个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
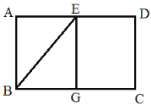
【题目】如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠,点A的对应点为点G.
(1)填空:如图1,当点G恰好在BC边上时,四边形ABGE的形状是___________形;
(2)如图2,当点G在矩形ABCD内部时,延长BG交DC边于点F.
![]() 求证:BF=AB+DF;
求证:BF=AB+DF;
![]() 若AD=
若AD=![]() AB,试探索线段DF与FC的数量关系.
AB,试探索线段DF与FC的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
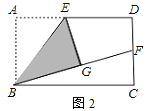
【题目】如图,抛物线y=x2﹣mx﹣3(m>0)交y轴于点C,CA⊥y轴,交抛物线于点A,点B在抛物线上,且在第一象限内,BE⊥y轴,交y轴于点E,交AO的延长线于点D,BE=2AC.
(1)用含m的代数式表示BE的长.
(2)当m= ![]() 时,判断点D是否落在抛物线上,并说明理由.
时,判断点D是否落在抛物线上,并说明理由.
(3)若AG∥y轴,交OB于点F,交BD于点G.
①若△DOE与△BGF的面积相等,求m的值.
②连结AE,交OB于点M,若△AMF与△BGF的面积相等,则m的值是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形纸片ABC中,点D在边AB(不包含端点A、B)上运动,连接CD,将∠ADC对折,点A落在直线CD上的点A′处,得到折痕DE;将∠BDC对折,点B落在直线CD上的点B′处,得到折痕DF.
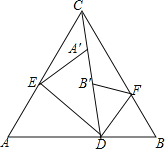
(1)若∠ADC=80°,求∠BDF的度数;
(2)试问∠EDF的大小是否会随着点D的运动而变化?若不变,求出∠EDF的大小;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数 ![]() ,下列结论中,不正确的是( )
,下列结论中,不正确的是( )
A.图象必经过点(1,2)
B.y随x的增大而增大
C.图象在第一、三象限内
D.若x>1,则0<y<2
查看答案和解析>>
科目:初中数学 来源: 题型:
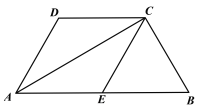
【题目】已知,四边形ABCD中,AB∥CD,AB=2CD,E为AB的中点,AC为对角线,AC⊥BC.
(1)求证:四边形AECD是菱形.
(2)若∠DAE=60°,AE=2,求菱形AECD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com