
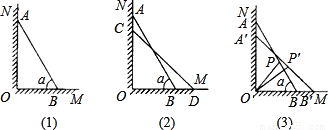
 =2(m)
=2(m)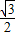 =2
=2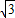 (m)
(m)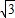 m.
m.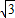 -2x,OD=2+3x,CD=4m.
-2x,OD=2+3x,CD=4m.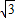 -2x)2+(2+3x)2=42.
-2x)2+(2+3x)2=42. )x=0.
)x=0. =0,
=0,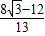 m.
m.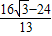 m.
m.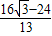 m.
m. =2
=2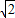 (m).
(m).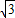 -2
-2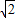 )m.
)m.

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案科目:初中数学 来源: 题型:
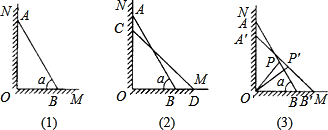 点P也随之运动到P′点,若∠POP′=15°,试求AA′的长.
点P也随之运动到P′点,若∠POP′=15°,试求AA′的长.查看答案和解析>>
科目:初中数学 来源:《第28章 锐角三角函数》2009年综合测试(解析版) 题型:解答题
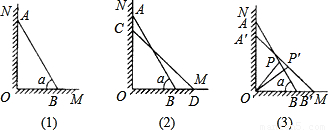
查看答案和解析>>
科目:初中数学 来源:第31章《锐角三角函数》常考题集(16):31.3 锐角三角函数的应用(解析版) 题型:解答题
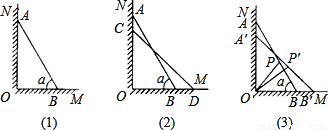
查看答案和解析>>
科目:初中数学 来源:2010年中考数学模拟卷(11)(解析版) 题型:解答题
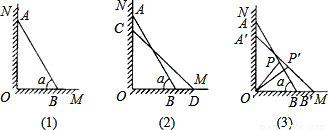
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com