Question

如图所示的一块地，∠ADC=90°，AD=12m，CD=9m，AB=39m，BC=36m，求这块地的面积．

Answer 1

解：连接AC，

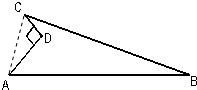
已知，在直角△ACD中，CD=9m，AD=12m，
根据AD²+CD²=AC²，可以求得AC=15m，
在△ABC中，AB=39m，BC=36m，AC=15m，
∴存在AC²+CB²=AB²，
∴△ABC为直角三角形，
要求这块地的面积，求△ABC和△ACD的面积之差即可，
S=S_△ABC-S_△ACD=AC•BC-CD•AD，
=×15×36-×9×12，
=270-54，
=216m²，
答：这块地的面积为216m²．
分析：连接AC，根据直角△ACD可以求得斜边AC的长度，根据AC，BC，AB可以判定△ABC为直角三角形，要求这块地的面积，求△ABC与△ACD的面积之差即可．
点评：本题考查了勾股定理在实际生活中的运用，考查了直角三角形面积的计算，本题中正确的判定△ABC是直角三角形是解题的关键．