
【题目】湖南师大附中组织集团校内七、八、九年级学生参加“12KM”作文比赛,该校将收到的参赛作文进行分年级统计,绘制了如图1和如图2两幅不完整的统计图,根据图中提供的信息完成以下问题.
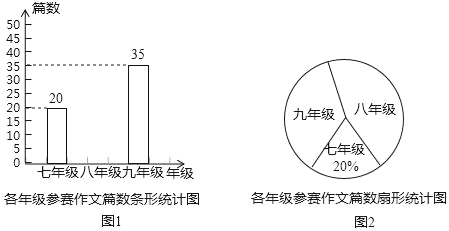
(1)扇形统计图中九年级参赛作文篇数对应的圆心角是 度.八年级参赛作文篇数对应的百分比是 .
(2)请补全条形统计图.
(3)经过评审,全集团校内有4篇作文荣获特等奖,其中一篇来自九年级,学校准备从特等奖作文中任选两篇刊登在校报上,请利用画树状图或列表的方法求出九年级特等奖作文被选登在校报上的概率.
【答案】(1) 126°,45%;(2)见解析;(3)![]() .
.
【解析】
(1)求出总的作文篇数,即可得出九年级参赛作文篇数对应的圆心角的度数;求出八年级的作文篇数,再用360°乘以对应比例可得;
(2)补全条形统计图即可;
(3)假设4篇荣获特等奖的作文分别为A、B、C、D,其中A代表九年级获奖的特等奖作文.列表求解即可得出答案.
(1)∵参赛作文的总数量为20÷20%=100(篇),∴九年级参赛作文篇数对应的圆心角是360°×![]() =126°,八年级的参赛数量为100﹣(20+35)=45(篇),则八年级参赛作文篇数对应的百分比是
=126°,八年级的参赛数量为100﹣(20+35)=45(篇),则八年级参赛作文篇数对应的百分比是![]() ×100%=45%;
×100%=45%;
(2)补全条形图如下:
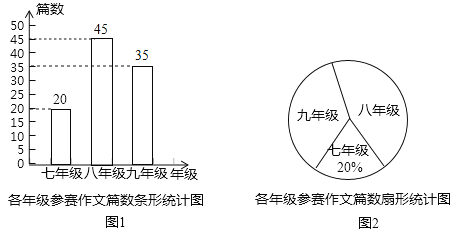
(3)假设4篇荣获特等奖的作文分别为A、B、C、D,列表如下:

由表格可知,共有12种可能性结果,它们发生的可能性相等,其中九年级特等奖作文被选登在校刊上的可能性有6种,所以九年级特等奖作文被选登在校报上的概率为![]() =
=![]() .
.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案科目:初中数学 来源: 题型:
【题目】某学校创客小组进行机器人跑步大赛,机器人小![]() 和小
和小![]() 从同一地点同时出发,小
从同一地点同时出发,小![]() 在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有_________ (填序号).
在跑到1分钟的时候监控到程序有问题,随即开始进行远程调试,到3分钟的时候调试完毕并加速前进,最终率先到达终点,测控小组记录的两个机器人行进的路程与时间的关系如图所示,则以下结论正确的有_________ (填序号).
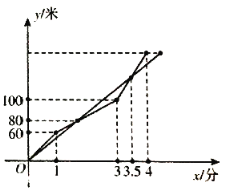
①两个机器人第一次相遇时间是在第2分钟;
②小![]() 每分钟跑50米;
每分钟跑50米;
③赛程总长200米;
④小![]() 到达终点的时候小
到达终点的时候小![]() 距离终点还有20米.
距离终点还有20米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数y=﹣x+2的图象与x轴,y轴分别交于点A,B,与函数y=![]() x+b的图象交于点C(﹣2,m).
x+b的图象交于点C(﹣2,m).
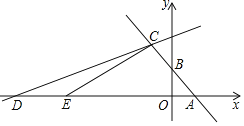
(1)求m和b的值;
(2)函数y=![]() x+b的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速运动到点A(到A停止运动).设点E的运动时间为t秒.
x+b的图象与x轴交于点D,点E从点D出发沿DA方向,以每秒2个单位长度匀速运动到点A(到A停止运动).设点E的运动时间为t秒.
①当△ACE的面积为12时,求t的值;
②在点E运动过程中,是否存在t的值,使△ACE为直角三角形?若存在,直接写出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为(-3,-6)的抛物线![]() 经过点(-1,-4),下列结论中错误的是( )
经过点(-1,-4),下列结论中错误的是( )

A. ![]()
B. 若点(-2, ![]() ),(-5,
),(-5, ![]() ) 在抛物线上,则
) 在抛物线上,则![]()
C. ![]()
D. 关于![]() 的一元二次方程
的一元二次方程![]() 的两根为-5和-1
的两根为-5和-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图![]() ,在以
,在以![]() 为原点的平面直角坐标系中,抛物线
为原点的平面直角坐标系中,抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() ,
,![]() ,直线
,直线![]() 过点
过点![]() 且平行于
且平行于![]() 轴,
轴,![]() ,
,
![]() 求抛物线对应的二次函数的解析式;
求抛物线对应的二次函数的解析式;
![]() 若
若![]() 为抛物线
为抛物线![]() 上一动点,是否存在直线
上一动点,是否存在直线![]() 使得点
使得点![]() 到直线
到直线![]() 的距离与
的距离与![]() 的长恒相等?若存在,求出此时
的长恒相等?若存在,求出此时![]() 的值;
的值;
![]() 如图
如图![]() ,若
,若![]() 、
、![]() 为上述抛物线上的两个动点,且
为上述抛物线上的两个动点,且![]() ,线段
,线段![]() 的中点为
的中点为![]() ,求点
,求点![]() 纵坐标的最小值.
纵坐标的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
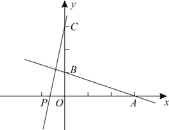
【题目】如图,一次函数![]() 的图象与
的图象与![]() 轴,
轴,![]() 轴分别交于
轴分别交于![]() ,
,![]() 两点,在
两点,在![]() 轴上有一点
轴上有一点![]() ,动点
,动点![]() 从
从![]() 点以每秒2个单位长度的速度向左移动,
点以每秒2个单位长度的速度向左移动,
(1)求直线![]() 的表达式;
的表达式;
(2)求![]() 的面积
的面积![]() 与移动时间
与移动时间![]() 之间的函数关系式;
之间的函数关系式;
(3)当![]() 为何值时,
为何值时,![]() ≌
≌![]() ,求出此时
,求出此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某乡在推进村村通公路某项目建设中,计划修建公路15千米.已知甲队单独完成修建公路所需得时间是乙队得1.5倍,甲队每天比乙队少修0.5千米.
(1)求甲、乙两队单独完成修建公路各需多少天?
(2)已知甲队每天的工作费用是4000元,乙队每天的工作费用是5000元,若该工程由甲乙两队合作完成,且工程的总费用不超过52000元,求乙队至少要工作多少天?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com