
ЁОЬтФПЁПЃЈ2015ЩНЖЋЪЁЕТжнЪаЃЌ24ЃЌ12ЗжЃЉвбжЊХзЮяЯпy=-mx2+4x+2mгыxжсНЛгкЕуAЃЈІСЃЌ0ЃЉЃЌ BЃЈІТЃЌ0ЃЉЃЌЧв![]() ЃЎ
ЃЎ
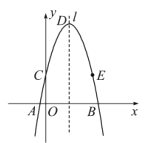
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЎ
ЃЈ2ЃЉХзЮяЯпЕФЖдГЦжсЮЊlЃЌгыyжсЕФНЛЕуЮЊCЃЌЖЅЕуЮЊDЃЌЕуCЙигкlЕФЖдГЦЕуЮЊEЃЎЪЧЗёДцдкxжсЩЯЕФЕуMЁЂyжсЩЯЕФЕуNЃЌЪЙЫФБпаЮDNMEЕФжмГЄзюаЁЃПШєДцдкЃЌЧыЛГіЭМаЮЃЈБЃСєзїЭМКлМЃЃЉЃЌВЂЧѓГіжмГЄЕФзюаЁжЕЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЃЈ3ЃЉШєЕуPдкХзЮяЯпЩЯЃЌЕуQдкxжсЩЯЃЌЕБвдЕуDЁЂEЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮЪЧЦНааЫФБпаЮЪБЃЌЧѓЕуPЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=-x2+4x+2ЃЛ
ЃЈ2ЃЉЫФБпаЮDNMEЕФжмГЄЕФзюаЁжЕЮЊ10+2![]()
ЃЈ3ЃЉЃЈ2-![]() ЃЌ4ЃЉЃЌЃЈ2+
ЃЌ4ЃЉЃЌЃЈ2+![]() ЃЌ4ЃЉЃЌЃЈ2+
ЃЌ4ЃЉЃЌЃЈ2+![]() ЃЌ-4ЃЉЃЌЃЈ2-
ЃЌ-4ЃЉЃЌЃЈ2-![]() ЃЌ-4ЃЉЃЎ
ЃЌ-4ЃЉЃЎ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉРћгУИљОнгыЯЕЪ§ЕФЙиЯЕЕУГіІС+ІТ=![]() ЃЌІСІТ=Љ2ЃЌНјЖјДњШыЧѓГіmЕФжЕМДПЩЕУГіД№АИЃЛ
ЃЌІСІТ=Љ2ЃЌНјЖјДњШыЧѓГіmЕФжЕМДПЩЕУГіД№АИЃЛ
ЃЈ2ЃЉРћгУжсЖдГЦЧѓзюЖЬТЗЯпЕФЗНЗЈЃЌзїЕуDЙигкyжсЕФЖдГЦЕуDЁфЃЌЕуEЙигкxжсЕФЖдГЦЕуEЁфЃЌЕУГіЫФБпаЮDNMEЕФжмГЄзюаЁЮЊЃКDЁфEЁф+DEЃЌНјЖјРћгУЙДЙЩЖЈРэЧѓГіМДПЩЃЛ
ЃЈ3ЃЉРћгУЦНааЫФБпаЮЕФХаЖЈгыаджЪНсКЯPЕузнзјБъЮЊЁР4ЃЌНјЖјЗжБ№ЧѓГіМДПЩЃЎ
НтЃКЃЈ1ЃЉгЩЬтвтПЩЕУЃКІСЃЌІТЪЧЗНГЬЉmx2+4x+2m=0ЕФСНИљЃЌгЩИљгыЯЕЪ§ЕФЙиЯЕПЩЕУЃЌ
ІС+ІТ=![]() ЃЌІСІТ=Љ2ЃЌ
ЃЌІСІТ=Љ2ЃЌ
Ёп![]() =Љ2ЃЌ
=Љ2ЃЌ
Ёр![]() =Љ2ЃЌМД
=Љ2ЃЌМД![]() =Љ2ЃЌ
=Љ2ЃЌ
НтЕУЃКm=1ЃЌ
ЙЪХзЮяЯпНтЮіЪНЮЊЃКy=Љx2+4x+2ЃЛ
ЃЈ2ЃЉДцдкxжсЩЯЕФЕуMЃЌyжсЩЯЕФЕуNЃЌЪЙЕУЫФБпаЮDNMEЕФжмГЄзюаЁЃЌ
Ёпy=Љx2+4x+2=ЉЃЈxЉ2ЃЉ2+6ЃЌ
ЁрХзЮяЯпЕФЖдГЦжсlЮЊx=2ЃЌЖЅЕуDЕФзјБъЮЊЃКЃЈ2ЃЌ6ЃЉЃЌ
гжЁпХзЮяЯпгыyжсНЛЕуCЕФзјБъЮЊЃКЃЈ0ЃЌ2ЃЉЃЌЕуEгыЕуCЙигкlЖдГЦЃЌ
ЁрEЕузјБъЮЊЃКЃЈ4ЃЌ2ЃЉЃЌ
зїЕуDЙигкyжсЕФЖдГЦЕуDЁфЃЌЕуEЙигкxжсЕФЖдГЦЕуEЁфЃЌ
дђDЁфЕФзјБъЮЊЃЛЃЈЉ2ЃЌ6ЃЉЃЌEЁфзјБъЮЊЃКЃЈ4ЃЌЉ2ЃЉЃЌ
СЌНгDЁфEЁфЃЌНЛxжсгкMЃЌНЛyжсгкNЃЌ
ДЫЪБЃЌЫФБпаЮDNMEЕФжмГЄзюаЁЮЊЃКDЁфEЁф+DEЃЌШчЭМ1ЫљЪОЃК
бгГЄEЁфEЃЌЁфDНЛгквЛЕуFЃЌдкRtЁїDЁфEЁфFжаЃЌDЁфF=6ЃЌEЁфF=8ЃЌ
дђDЁфEЁф=![]() =
=![]() =10ЃЌ
=10ЃЌ
ЩшЖдГЦжсlгыCEНЛгкЕуGЃЌдкRtЁїDGEжаЃЌDG=4ЃЌEG=2ЃЌ
ЁрDE=![]() =
=![]() =2
=2![]() ЃЌ
ЃЌ
ЁрЫФБпаЮDNMEЕФжмГЄзюаЁжЕЮЊЃК10+2![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌPЮЊХзЮяЯпЩЯЕФЕуЃЌЙ§ЕуPзїPHЁЭxжсЃЌДЙзуЮЊHЃЌ
ШєвдЕуDЁЂEЁЂPЁЂQЮЊЖЅЕуЕФЫФБпаЮЮЊЦНааЫФБпаЮЃЌдђЁїPHQЁеЁїDGEЃЌ
ЁрPH=DG=4ЃЌ
Ёр|y|=4ЃЌ
ЁрЕБy=4ЪБЃЌЉx2+4x+2=4ЃЌ
НтЕУЃКx1=2+![]() ЃЌx2=2Љ
ЃЌx2=2Љ![]() ЃЌ
ЃЌ
ЕБy=Љ4ЪБЃЌЉx2+4x+2=Љ4ЃЌ
НтЕУЃКx3=2+![]() ЃЌx4=2Љ
ЃЌx4=2Љ![]() ЃЌ
ЃЌ
ЙЪPЕуЕФзјБъЮЊЃЛЃЈ2Љ![]() ЃЌ4ЃЉЃЌЃЈ2+
ЃЌ4ЃЉЃЌЃЈ2+![]() ЃЌ4ЃЉЃЌЃЈ2Љ
ЃЌ4ЃЉЃЌЃЈ2Љ![]() ЃЌЉ4ЃЉЃЌЃЈ2+
ЃЌЉ4ЃЉЃЌЃЈ2+![]() ЃЌЉ4ЃЉЃЎ
ЃЌЉ4ЃЉЃЎ
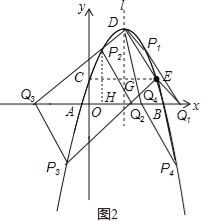


 УЯНЈЦНаЁбЇЙіЖЏВтЪдЯЕСаД№АИ
УЯНЈЦНаЁбЇЙіЖЏВтЪдЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЁбO ЕФжБОЖЮЊ 4ЃЌAB ЪЧЁбO ЕФЯвЃЌЁЯAOB=120ЁуЃЌЕу P дкЁбO ЩЯЃЌШєЕу PЕНжБЯп AB ЕФОрРыЮЊ 1ЃЌдђЁЯPAB ЕФЖШЪ§ЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдке§ЗНаЮABCDжаЃЌЖдНЧЯпBDЫљдкЕФжБЯпЩЯгаСНЕуEЁЂFТњзуBE=DFЃЌСЌНгAEЁЂAFЁЂCEЁЂCFЃЌШчЭМЫљЪОЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїABEЁеЁїADFЃЛ
ЃЈ2ЃЉЪдХаЖЯЫФБпаЮAECFЕФаЮзДЃЌВЂЫЕУїРэгЩЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌDEЁЭABЃЌBFЁЭCDЃЌДЙзуЗжБ№ЮЊEЃЌFЃЎ
ЃЈ1ЃЉЧѓжЄЃКЁїADEЁеЁїCBFЃЛ
ЃЈ2ЃЉЧѓжЄЃКЫФБпаЮBFDEЮЊОиаЮЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌгавЛПщжБНЧШ§НЧаЮжНЦЌЃЌСНжБНЧБпABЃН6ЃЌBCЃН8ЃЌНЋЁїABCелЕўЃЌЪЙABТфдкаББпACЩЯЃЌелКлЮЊADЃЌдђBDЕФГЄЮЊ(ЁЁ)

A. 6B. 5C. 4D. 3
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвЛСОПЭГЕДгМзЕиПЊЭљввЕиЃЌвЛСОГізтГЕДгввЕиПЊЭљМзЕиЃЌСНГЕЭЌЪБГіЗЂЃЌЫќУЧРыМзЕиЕФТЗГЬyЃЈkmЃЉгыПЭГЕааЪЛЪБМфxЃЈhЃЉМфЕФКЏЪ§ЙиЯЕШчЭМЃЌЯТСааХЯЂЃК
ЃЈ1ЃЉГізтГЕЕФЫйЖШЮЊ100ЧЇУз/ЪБЃЛ
ЃЈ2ЃЉПЭГЕЕФЫйЖШЮЊ60ЧЇУз/ЪБЃЛ
ЃЈ3ЃЉСНГЕЯргіЪБЃЌПЭГЕааЪЛСЫ3.75аЁЪБЃЛ
ЃЈ4ЃЉЯргіЪБЃЌГізтГЕРыМзЕиЕФТЗГЬЮЊ225ЧЇУзЃЎ
Цфжае§ШЗЕФИіЪ§гаЃЈЁЁЁЁЃЉ
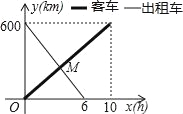
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
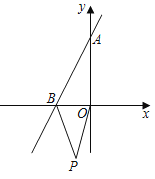
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃН2x+4ЗжБ№гыxжсЃЌyжсНЛгкBЃЌAСНЕу
ЃЈ1ЃЉЧѓЁїABOЕФУцЛ§ЃЛ
ЃЈ2ЃЉШчЙћдкЕкШ§ЯѓЯоФкгавЛЕуP(Љ1ЃЌm)ЃЌЧыгУКЌmЕФЪНзгБэЪОЫФБпаЮAOPBЕФУцЛ§ЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌЪЧЗёДцдкЕуPЃЌЪЙЫФБпаЮAOPBЕФУцЛ§ЪЧЁїABOУцЛ§ЕФ2БЖЃПШєДцдкЃЌЧыЧѓГіЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌDЪЧЕШБпЁїABCЕФABБпЩЯЕФвЛЖЏЕуЃЈВЛгыЖЫЕуAЁЂBжиКЯЃЉЃЌвдCDЮЊвЛБпЯђЩЯзїЕШБпЁїEDCЃЌСЌНгAEЃЎ

ЃЈ1ЃЉЮоТлDЕудЫЖЏЕНЪВУДЮЛжУЃЌЭМжазмгавЛЖдШЋЕШЕФШ§НЧаЮЃЌЧыевГіетвЛЖдШ§НЧаЮЃЌВЂжЄУїФуЕУГіЕФНсТлЃЛ
ЃЈ2ЃЉDЕудкдЫЖЏЙ§ГЬжаЃЌжБЯпAEгыBCЪМжеБЃГждѕбљЕФЮЛжУЙиЯЕ?ВЂЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
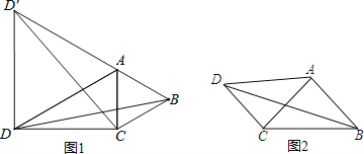
ЁОЬтФПЁПШчЭМЃЌдкЁїACDжаЃЌAD=9ЃЌCD=3![]() ЃЌЁїABCжаЃЌAB=ACЃЎ
ЃЌЁїABCжаЃЌAB=ACЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєЁЯCAB=60ЁуЃЌЁЯADC=30ЁуЃЌдкЁїACDЭтзїЕШБпЁїADDЁф
ЂйЧѓжЄЃКBD=CDЁфЃЛ
ЂкЧѓBDЕФГЄЃЎ
ЃЈ2ЃЉШчЭМ2ЃЌШєЁЯCAB=90ЁуЃЌЁЯADC=45ЁуЃЌЧѓBDЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com