
����Ŀ����ͼ����֪������y����![]() +bx+c��ͼ����A(��1��0)�͵�C(0��2)����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ(m��0)������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M.
+bx+c��ͼ����A(��1��0)�͵�C(0��2)����D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ(m��0)������P��x��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M.
(1)�������������ʾ�Ķ��κ����ı���ʽ.
(2)��֪��F(0��![]() )������P��x�����������˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
)������P��x�����������˶�ʱ������mΪ��ֵʱ���ı���DMQF��ƽ���ı��Σ�
(3)��P���߶�AB�˶������У��Ƿ���ڵ�Q��ʹ���Ե�B��Q��MΪ��������������BOD���ƣ������ڣ������Q�����ꣻ�������ڣ���˵������.
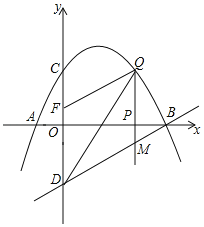
���𰸡�(1)![]() ��(2) m��3��m��1+
��(2) m��3��m��1+![]() �� (3)���ڣ���Q������Ϊ(3��2)��(��1��0)
�� (3)���ڣ���Q������Ϊ(3��2)��(��1��0)
��������
(1)���ô���ϵ����ȷ����������ʽ��
(2)�����ô���ϵ�������ֱ��BD����ʽΪy��![]() x��2����Q(m����
x��2����Q(m����![]() m2+
m2+![]() m+2)��M(m��
m+2)��M(m��![]() m��2)����QM��DF���ı���DMQF��ƽ���ı���֪QM��DF��������������ٵ���P���߶�AB��ʱ�ڵ�P��AB���ӳ�����ʱ���ֱ��г�����m�ķ��̣���֮�ɵã�
m��2)����QM��DF���ı���DMQF��ƽ���ı���֪QM��DF��������������ٵ���P���߶�AB��ʱ�ڵ�P��AB���ӳ�����ʱ���ֱ��г�����m�ķ��̣���֮�ɵã�
(3)��֪��ODB����QMB���ʷ֢١�DOB����MBQ��90�������á�DOB�ס�MBQ��![]() ��
��![]() ����֤��MBQ�ס�BPQ��
����֤��MBQ�ס�BPQ��![]() ����
����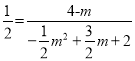 ����֮���ɵô�ʱm��ֵ���ڡ�BQM��90������ʱ��Q���A�غϣ���BOD�ס�BQM�����õ�Q����.
����֮���ɵô�ʱm��ֵ���ڡ�BQM��90������ʱ��Q���A�غϣ���BOD�ס�BQM�����õ�Q����.
(1)����A(��1��0)�͵�C(0��2)����y����![]() x2+bx+c�У���
x2+bx+c����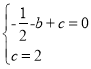 .
.
���![]() .
.
��������߽���ʽΪ��![]() ��
��
(2) ������֪��D����Ϊ(0����2)��
�ߵ�B����������x��������Ľ��㣬��![]() ��
��
���x=4��x=-1����ȥ����
��B������4��0����
��ֱ��BD����ʽΪy��kx+b��
��B(4��0)��D(0����2)���룬�ã�![]() ��
��
��ã�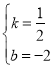 ��
��
��ֱ��BD����ʽΪy��![]() x��2��
x��2��
���������������
�ٵ���P���߶�AB��ʱ��
��QM��x�ᣬP(m
��Q(m����![]() m2+
m2+![]() m+2)��M(m��
m+2)��M(m��![]() m��2)��
m��2)��
��QM����![]() m2+
m2+![]() m+2��(
m+2��(![]() m��2)����
m��2)����![]() m2+m+4��
m2+m+4��
��F(0��![]() )��D(0����2)��
)��D(0����2)��
��DF��![]() ��
��
��QM��DF��
�൱��![]() m2+m+4��
m2+m+4��![]() ʱ���ı���DMQF��ƽ���ı��Σ�
ʱ���ı���DMQF��ƽ���ı��Σ�
��ã�m����1��m��3��
��m��0��
��m=3��
����m��3ʱ���ı���DMQF��ƽ���ı��Σ�
�ڵ�P��AB���ӳ�����ʱ��
��QM��x�ᣬP(m��0)(m��0)��
��Q(m����![]() m2+
m2+![]() m+2)��M(m��
m+2)��M(m��![]() m��2)��
m��2)��
��QM��![]() m��2��(��
m��2��(��![]() m2+
m2+![]() m+2)��
m+2)��![]() m2��m��4��
m2��m��4��
��F(0��![]() )��D(0����2)��
)��D(0����2)��
��DF��![]() ��
��
��QM��DF��
�൱![]() m2��m��4��
m2��m��4��![]() ʱ���ı���DMQF��ƽ���ı��Σ�
ʱ���ı���DMQF��ƽ���ı��Σ�
���m��![]() ��
��
��m��0��
��m��1+![]() ��
��
����m��1+![]() ʱ���ı���DMQF��ƽ���ı��Σ�
ʱ���ı���DMQF��ƽ���ı��Σ�
������������m��3��m��1+![]() ʱ���ı���DMQF��ƽ���ı��Σ�
ʱ���ı���DMQF��ƽ���ı��Σ�
(3)��ͼ��ʾ��
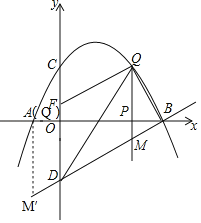
��QM��DF��
���ODB����QMB��
���������������
�ٵ���DOB����MBQ��90��ʱ����DOB�ס�MBQ��
��![]() ��
��
�ߡ�MBQ��90����
���MBP+��PBQ��90����
�ߡ�MPB����BPQ��90����
���MBP+��BMP��90����
���BMP����PBQ��
���MBQ�ס�BPQ��
��![]() ����
����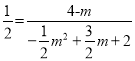 ��
��
��ã�m1��3��m2��4��
��m��4ʱ����P��Q��M�����B�غϣ����ܹ��������Σ���ȥ��
��m��3����Q������Ϊ(3��2)��
�ڵ���BQM��90��ʱ����ʱ��Q���A�غϣ���BOD�ס�BQM����
��ʱm����1����Q������Ϊ(��1��0)��
���ϣ���Q������Ϊ(3��2)��(��1��0)ʱ���Ե�B��Q��MΪ��������������BOD����.


 ѧҵ����һ��һ��ϵ�д�
ѧҵ����һ��һ��ϵ�д� Сѧ��ʱ��ҵȫͨ����ϵ�д�
Сѧ��ʱ��ҵȫͨ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��ҡ���������λͬѧ����һ��ƹ���������Ҫ����ѡ����λͬѧ���һ������.
��1��������״ͼ�����б�������ǡ��ѡ�мס�����λͬѧ�ĸ���.
��2������ȷ���״��һ�����ٴ�������λͬѧ�����ѡȡһλ����ǡ��ѡ����ͬѧ�ĸ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��������һ����Ʒ���ɱ���Ϊ20Ԫ/ǧ�ˣ����г����飬ÿ��������y(ǧ��)�����۵���x(Ԫǧ��)֮��Ĺ�ϵ��ͼ��ʾ���涨ÿǧ���ۼ۲��ܵ���30Ԫ���Ҳ�����80Ԫ��
(1)ֱ��д��y��x֮��ĺ�����ϵʽ��
(2)����ó�������������Ʒÿ����3900Ԫ��������ô����Ʒ�����۵���Ϊ����Ԫ��
(3)��ÿ���������ΪwԪ�������۵��۶�Ϊ����Ԫʱ���ó���ÿ������������������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
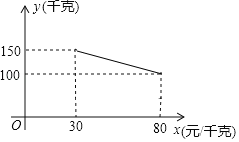
����Ŀ����ͼ����ABC�У�AB=AC����E��F�ڱ�BC�ϣ�BE=CF����D��AF���ӳ����ϣ�AD=AC��
��1����֤����ABE�ա�ACF��
��2������BAE=30�������ADC=�� ���㣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����һ��С������ǽƽ��ͣ�ŵ�ƽ��ʾ��ͼ��������ǽһ��OB��ǽMNƽ���Ҿ���Ϊ0.8�ף�һ��С�������ſ�AOΪ1.2�ף������ŴǶȡ�AOBΪ40��ʱ�������Ƿ������ǽ��______��(��ǡ���)������������_______��(�ο����ݣ�sin40���0.64��cos40���0.77��tan40���0.84)
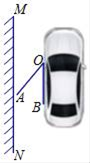
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,AB�ǰ�ԲԲO��ֱ��,C�ǻ�AB���е�,M����AC���е�,CH��BM,����ΪH.��֤
��1����AHO=90��
��2����֤��CH=AHOH.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ھ���ABCD�У���CD��5����DΪԲ�ģ�DC��Ϊ�뾶����D��CA���ӳ�����E����D��DF��AC������ΪF����DF��3��
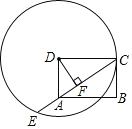
��1����֤��BC�ǡ�D�����ߣ�
��2����AE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��֣������������ȥũó�г�����̯����֣���̵�Ҫ���õ��ӳӳ���5ǧ�˼�����֣���̻����������ԣ��Ѽ��������Դ�������Ϊ0.6ǧ�˵������У���������ȷ����Ҫ����ڵ��ӳ����ٳ�һ�飬�Ƶ�Ϊ5.75ǧ�ˣ��ϰ������˵������ȥ���Ӻ�Ϊ5.15ǧ�ˣ��Ϲ˿�������0.15ǧ�˾����ˡ���֣���̸��˵ظ���Ǯ������ػؼ��ˡ�����˵����ȷ���ǣ� ��

A.֣�����ˣ�������ʵ������Ϊ5.15ǧ��
B.֣���̿��ˣ�������ʵ������Ϊ4ǧ��
C.֣���̿��ˣ�������ʵ������Ϊ4.85ǧ��
D.֣���̲���Ҳ����������ʵ������Ϊ5ǧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
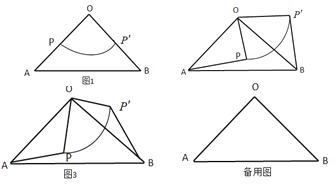
����Ŀ����ͼ1��![]() �У�
��![]() ��������
��������![]() ��ͼ1�ڷţ�ʹ���εİ뾶
��ͼ1�ڷţ�ʹ���εİ뾶![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() �غϣ�
�غϣ�![]() ��
��
����������
��ͼ2����![]() ������������
������������![]() �Ƶ�
�Ƶ�![]() ��ʱ����תһ�ܣ������߶�
��ʱ����תһ�ܣ������߶�![]() ��
��![]() ������ת��Ϊ
������ת��Ϊ![]() ��
��
���֣�ֱ��д��![]() ��
��![]() ��������ϵ��
��������ϵ��
̽������![]()
��1������![]() �Ƶ���
�Ƶ���![]() ����࣬��
����࣬��![]() ʱ����ת��
ʱ����ת��![]() ______�㣻
______�㣻
��2������![]() �Ƶ���
�Ƶ���![]() ���Ҳ࣬��
���Ҳ࣬��![]() ��
��![]() ����ʱ����
����ʱ����![]() ��
��
��3������![]() �ǻ�
�ǻ�![]() ������һ�㣬������
������һ�㣬������![]() �Ƶ�
�Ƶ�![]() ��ʱ��ת�����У���
��ʱ��ת�����У���![]() ��������ʱ��ֱ��д��
��������ʱ��ֱ��д��![]() �Ķ�����
�Ķ�����
���죺��ͼ3����![]() ����
����![]() ��
��![]() ��
��![]() ���㹲��ʱ��ֱ��д���߶�
���㹲��ʱ��ֱ��д���߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com