
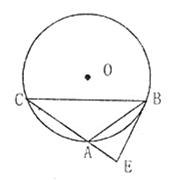
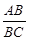 =
=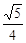 时,①求tan∠ABE的值;②如果AE=
时,①求tan∠ABE的值;②如果AE=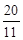 ,求AC的值。
,求AC的值。

 ∴
∴ ∴
∴ …………………….….…….4分
…………………….….…….4分 ,
, ,
, =
= ………………5分
………………5分 ……………………………6分
……………………………6分 EBA和
EBA和 ECB中,
ECB中,  =
=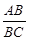 ……………………………7分
……………………………7分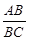 =
=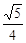
 (※)…………………8分
(※)…………………8分
 …………………………9分
…………………………9分 ,
, ………………………………………………10分
………………………………………………10分 ,转化为求AF的问题.
,转化为求AF的问题.

 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案科目:初中数学 来源:不详 题型:单选题
| A.(2,-1)或(-2,1) | B.(8,-4)或(-8,4) | C.(2,-1) | D.(8,-4) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.都扩大为原来的5倍 | B.都扩大为原来的10倍 |
| C.都扩大为原来的25倍 | D.都与原来相等 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
 ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,AB=AC.四边形PQRS是正方形。
ABC的高,点P,Q在BC边上,点R在AC边上,点S在AB边上,BC=60cm,AD=40cm,AB=AC.四边形PQRS是正方形。 ASR与
ASR与 ABC相似吗?为什么?
ABC相似吗?为什么?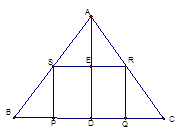
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com