
【题目】已知:如图,在△ABC中,AB=AC,AD⊥BC,垂足为点D,AN是△ABC外角∠CAM的平分线,CE⊥AN,垂足为点E,
(1)求证:四边形ADCE为矩形;
(2)当△ABC满足什么条件时,四边形ADCE是一个正方形?并给出证明.

【答案】(1)(2)见解析
【解析】
试题(1)求出∠BAD=∠DAC,∠MAE=∠CAE,求出∠DAE的度数,求出∠AEC=∠ADC=∠EAD=90°,根据矩形的判定判断即可;
(2)求出AD=DC,得出∠ACD=∠DAC=45°,求出∠BAC=90°,即可求出答案.
试题解析:(1)证明:∵在△ABC中,AB=AC,AD⊥BC,
∴∠BAD=∠DAC,
∵AN是△ABC外角∠CAM的平分线,
∴∠MAE=∠CAE.
∴∠DAE=∠DAC+∠CAE=![]() ∠MAC+
∠MAC+![]() ∠CAB=
∠CAB=![]() ×180°=90°,
×180°=90°,
又∵AD⊥BC,CE⊥AN,
∴∠ADC=∠CEA=90°,
∴四边形ADCE为矩形.
(2)证明:∵四边形ADCE是正方形,
∴DC=AD,
∵在△ABC中,AB=AC,AD⊥BC,
∴△ADC为等腰直角三角形,
∴∠DAC=∠ACD=45°,
∴∠BAC=90°,
∴△ABC为等腰直角三角形,
即△ABC的形状是等腰直角三角形.


 优等生题库系列答案
优等生题库系列答案 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
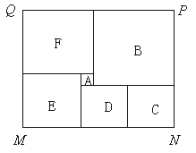
【题目】如图是某市民健身广场的平面示意图,它是由6个正方形拼成的长方形,已知中间最小的正方形A的边长是1米.
(1)若设图中最大正方形B的边长是x米,请用含x的代数式分别表示出:
正方形F的边长= 米;正方形E的边长= 米;正方形C的边长= 米;
(2)观察图形的特点可知,长方形相对的两边是相等的(如图中的MN=PQ).根据等量关系可求出x= ;
(3)现沿着长方形广场的四条边铺设下水管道,由甲、乙2个工程队单独铺设分别需要10天、15天完成.如果两队从同一点开始,沿相反的方向同时施工2天后,因甲队另有任务,余下的工程由乙队单独施工,试问乙还要多少天完成?甲、乙2个工程队各铺设多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(背景)如图(a),△ABC与△ADE均是顶角为40°的等腰三角形,BC,DE分别是底边,求证:BD=CE.
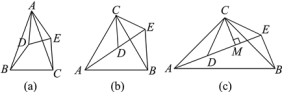
(探究)如图(b),△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.
①∠AEB的度数为________;②线段BE与AD之间的数量关系是________.
(拓展)如图(c),△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE.
①求∠AEB的度数;
②请直接写出线段CM,AE,BE之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知平行四边形ABCD的顶点A在第三象限,对角线AC的中点在坐标原点,一边AB与x轴平行且AB=2,若点A的坐标为(a,b),则点D的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次综合实践活动中,小明要测某地一座古塔AE的高度.如图,已知塔基顶端B(和A、E共线)与地面C处固定的绳索的长BC为80m.她先测得∠BCA=35°,然后从C点沿AC方向走30m到达D点,又测得塔顶E的仰角为50°,求塔高AE.(人的高度忽略不计,结果用含非特殊角的三角函数表示)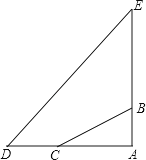
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个小组同时从甲地出发,匀速步行到乙地,甲乙两地相距7500米,第一组的步行速度是第二组的1.2倍,并且比第二组早15分钟到达乙地.设第二组的步行速度为x千米/小时,根据题意可列方程是( )
A.![]() ﹣
﹣ ![]() =15
=15
B.![]() ﹣
﹣ ![]() =
= ![]()
C.![]() ﹣
﹣ ![]() =15
=15
D.![]() ﹣
﹣ ![]() =
= ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com