
(3分)如图,若长方形APHM,BNHP,CQHN的面积分别为7、4、6,求阴影部分的面积是多少?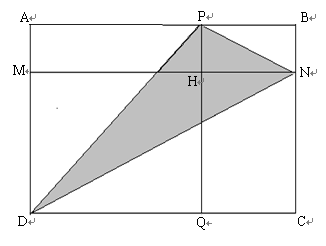
8.5
解析考点:面积及等积变换。
分析:设HQ交DN于O,根据长方形APHM,BNHP,CQHN的面积可求出各个线段之间的比,最终求出PH:HO的值,然后根据三角形面积公式求出阴影部分的面积。
解答:
设四边形MHQD的面积为x,
∵长方形APHM,BNHP,CQHN的面积分别为7、4、6,
∴7:4=x:6,
x=10.5,
∴四边形ABCD的面积为:4+7+6+10.5=27.5,
S△PDN=27.5-S△ADP-S△PBN-S△DNC=27.5-1/2(4+7+10.5+6+10.5)=8.5。
点评:本题主要考查面积及等积变换的知识点,解答本题的关键是根据长方形APHM,BNHP,CQHN的面积求出相关线段的比值,本题难度不是很大。


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源:2009-2010年江西省上饶市横峰县七年级数学竞赛 题型:解答题
(3分)如图,若长方形APHM,BNHP,CQHN的面积分别为7、4、6,求阴影部分的面积是多少?
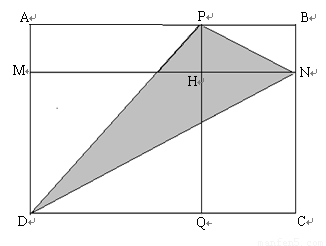
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com