
【题目】已知∠AOB=α(90°<α<180°),∠COD在∠AOB的内部,OM平分∠AOC,ON平分∠BOD. 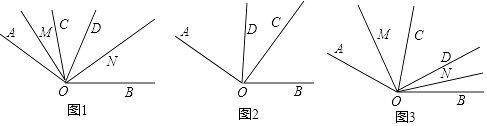
(1)若∠COD=180°﹣α时,探索下面两个问题: ①如图1,当OC在OD左侧,求∠MON的度数;
②当OC在OD右侧,请在图2内补全图形,并求出∠MON的度数(用含α的代数式表示);
(2)如图3,当∠COD=kα,且OC在OD左侧时,直接写出∠MON的度数(用含α、k的代数式表示).
【答案】
(1)解:①如图1,

∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM= ![]() ∠AOC,∠BON=
∠AOC,∠BON= ![]() ∠BOD,
∠BOD,
∴∠AOM+∠BON= ![]() (∠AOC+∠BOD),
(∠AOC+∠BOD),
∵∠AOB=α,∠COD=180°﹣α,
∴∠AOC+∠BOD=∠AOB﹣∠COD=α﹣(180°﹣α)=2α﹣180°,
∴∠AOM+∠BON= ![]() (2α﹣180°)=α﹣90°,
(2α﹣180°)=α﹣90°,
∴∠MON=∠AOB﹣(∠AOM+∠BON)=α﹣(α﹣90°)=90°
②当OC在OD右侧,补全图形如图2所画,

∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM= ![]() ∠AOC,∠BON=
∠AOC,∠BON= ![]() ∠BOD,
∠BOD,
∵∠AOB=α,∠COD=180°﹣α,
∴∠AOC+∠BOD=∠AOB+∠COD=α+(180°﹣α)=180°,
∴∠AOM+∠BON= ![]() ×180°=90°,
×180°=90°,
∴∠MON=∠AOB﹣(∠AOM+∠BON)=α﹣90°
(2)解:∠MON的度数为 ![]() (1+k)α.
(1+k)α.
理由:如图3,
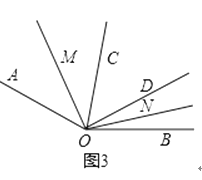
∵OM平分∠AOC,ON平分∠BOD,
∴∠AOM= ![]() ∠AOC,∠BON=
∠AOC,∠BON= ![]() ∠BOD,
∠BOD,
∴∠AOM+∠BON= ![]() (∠AOC+∠BOD),
(∠AOC+∠BOD),
∵∠AOB=α,∠COD=kα,
∴∠AOC+∠BOD=∠AOB﹣∠COD=α﹣kα,
∴∠AOM+∠BON= ![]() (α﹣kα)=
(α﹣kα)= ![]() α(1﹣k),
α(1﹣k),
∴∠MON=∠AOB﹣(∠AOM+∠BON)=α﹣ ![]() α(1﹣k)=
α(1﹣k)= ![]() (1+k)α
(1+k)α
【解析】(1)①根据角平分线的定义,得出∠AOM= ![]() ∠AOC,∠BON=
∠AOC,∠BON= ![]() ∠BOD,再根据∠AOB=α,∠COD=180°﹣α,得出∠AOC+∠BOD=∠AOB﹣∠COD=α﹣(180°﹣α)=2α﹣180°,进而得出∠AOM+∠BON=
∠BOD,再根据∠AOB=α,∠COD=180°﹣α,得出∠AOC+∠BOD=∠AOB﹣∠COD=α﹣(180°﹣α)=2α﹣180°,进而得出∠AOM+∠BON= ![]() (2α﹣180°)=α﹣90°,最后根据∠MON=∠AOB﹣(∠AOM+∠BON)进行计算即可;②根据①中的方法进行计算,即可得出∠MON的度数;(2)先根据角平分线的定义,得出∠AOM=
(2α﹣180°)=α﹣90°,最后根据∠MON=∠AOB﹣(∠AOM+∠BON)进行计算即可;②根据①中的方法进行计算,即可得出∠MON的度数;(2)先根据角平分线的定义,得出∠AOM= ![]() ∠AOC,∠BON=
∠AOC,∠BON= ![]() ∠BOD,再根据∠AOB=α,∠COD=kα,得出∠AOC+∠BOD=∠AOB﹣∠COD=α﹣kα,进而得到∠AOM+∠BON=
∠BOD,再根据∠AOB=α,∠COD=kα,得出∠AOC+∠BOD=∠AOB﹣∠COD=α﹣kα,进而得到∠AOM+∠BON= ![]() (α﹣kα)=
(α﹣kα)= ![]() α(1﹣k),最后根据∠MON=∠AOB﹣(∠AOM+∠BON)进行计算即可.
α(1﹣k),最后根据∠MON=∠AOB﹣(∠AOM+∠BON)进行计算即可.
【考点精析】解答此题的关键在于理解角的平分线的相关知识,掌握从一个角的顶点引出的一条射线,把这个角分成两个相等的角,这条射线叫做这个角的平分线,以及对角的运算的理解,了解角之间可以进行加减运算;一个角可以用其他角的和或差来表示.


 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:
【题目】如图(1),将两块直角三角板的直角顶点C叠放在一起. 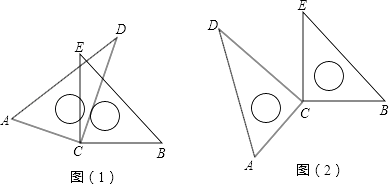
(1)试判断∠ACE与∠BCD的大小关系,并说明理由;
(2)若∠DCE=30°,求∠ACB的度数;
(3)猜想∠ACB与∠DCE的数量关系,并说明理由;
(4)若改变其中一个三角板的位置,如图(2),则第(3)小题的结论还成立吗?(不需说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=﹣x2+6x+c的图象过点A(﹣1,y1),B(1,y2),C(4,y3)三点,则y1 , y2 , y3的大小关系是( )
A.y1>y2>y3
B.y2>y1>y3
C.y3>y2>y1
D.y3>y1>y2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地驶向B地,并以各自的速度匀速行驶,甲车比乙车早行驶2 h,并且甲车途中休息了0.5 h,如图是甲、乙两车行驶的路程y(km)与时间x(h)的函数图象.
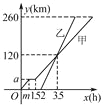
(1)求出图中m和a的值.
(2)求出甲车行驶的路程y(km)与时间x(h)的函数关系式,并写出相应的x的取值范围.
(3)当乙车行驶多长时间时,两车恰好相距50 km?
查看答案和解析>>
科目:初中数学 来源: 题型:
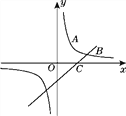
【题目】如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(1)求该反比例函数的表达式;
(2)求直线BC的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com