
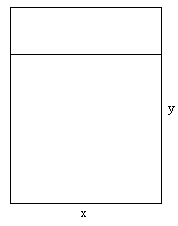
如图,用一根6m长的铝合金材料,做一个可分为上下两部分矩形窗框,求长和宽各是多少时,才能使通过的光线最多?
科目:初中数学 来源: 题型:
| 3.36 |
| 3.64 |
| 4.39 |
查看答案和解析>>
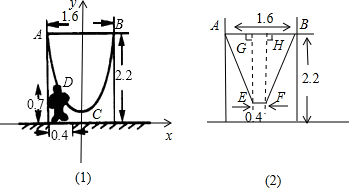
科目:初中数学 来源:第2章《二次函数》常考题集(18):2.6 何时获得最大利润(解析版) 题型:解答题
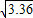 ≈1.8,
≈1.8,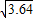 ≈1.9,
≈1.9,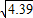 ≈2.1)
≈2.1)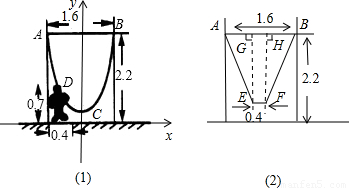
查看答案和解析>>
科目:初中数学 来源:第6章《二次函数》常考题集(19):6.4 二次函数的应用(解析版) 题型:解答题
 ≈1.8,
≈1.8,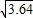 ≈1.9,
≈1.9,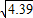 ≈2.1)
≈2.1)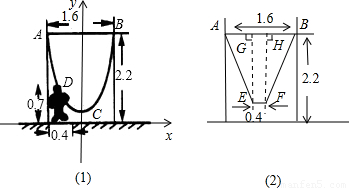
查看答案和解析>>
科目:初中数学 来源:第20章《二次函数和反比例函数》常考题集(19):20.5 二次函数的一些应用(解析版) 题型:解答题
 ≈1.8,
≈1.8,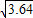 ≈1.9,
≈1.9,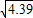 ≈2.1)
≈2.1)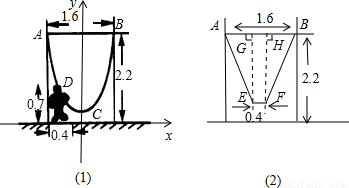
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com