
分析 (1)根据该校购买树苗的总费用为y(元),所购买樱花树苗为x(棵),可得购买白玉兰树苗的数量为(40-x)棵,据此即可得到y与x之间的函数关系式;
(2)根据购买樱花树苗的数量不超过白玉兰树苗的3倍,求得x的取值范围,再根据一次函数的性质,即可得到总费用最少的一种购买方案.
解答 解:(1)由题可得,y=100x+130(40-x)=-30x+5200;
(2)∵购买樱花树苗的数量不超过白玉兰树苗的3倍,
∴x≤3(40-x),
解得x≤30,
∵-30<0,
∴y随着x增大而减小,
∴当x取最大值时,y有最小值,
即当x=30时,ymin=-30×30+5200=4300,
∴当购买樱花树苗为30棵,白玉兰树苗10棵时,总费用最少最少为4300元.
点评 本题主要考查了一次函数以及一元一次不等式的应用,由实际问题中的不等关系列出不等式,建立解决问题的数学模型,通过解不等式可以得到实际问题的答案.解决问题的关键是读懂题意,找到关键描述语,进而找到所求的量的等量关系和不等关系.


科目:初中数学 来源: 题型:解答题
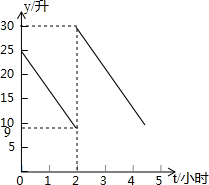 张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.
张师傅驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)之间的关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即沿原路按某一速度匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.
小明和爸爸进行登山锻炼,两人同时从山脚下出发,沿相同路线匀速上山,小明用8分钟登上山顶,此时爸爸距出发地280米.小明登上山顶立即沿原路按某一速度匀速下山,与爸爸相遇后,和爸爸一起以原下山速度返回出发地.小明、爸爸在锻炼过程中离出发地的路程y1(米)、y2(米)与小明出发的时间x(分)的函数关系如图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
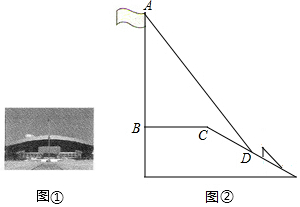 深圳市民中心广场上有旗杆如图①所示,某学校兴趣小组测量了该旗杆的高度,如图②,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为16米,落在斜坡上的影长CD为8米,AB⊥BC;同一时刻,太阳光线与水平面的夹角为45°.1米的标杆EF竖立在斜坡上的影长FG为2米,求旗杆的高度.
深圳市民中心广场上有旗杆如图①所示,某学校兴趣小组测量了该旗杆的高度,如图②,某一时刻,旗杆AB的影子一部分落在平台上,另一部分落在斜坡上,测得落在平台上的影长BC为16米,落在斜坡上的影长CD为8米,AB⊥BC;同一时刻,太阳光线与水平面的夹角为45°.1米的标杆EF竖立在斜坡上的影长FG为2米,求旗杆的高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
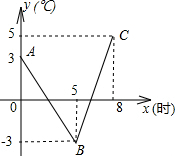 一种大棚蔬菜处在0℃以下的气温条件下超过3h,就会遭受冻害,秋末某天,该地区气象台发布如下的降温预报:由0时至次曰8时,气温y(℃)与时刻x(h)的函数关系如图中折线A-B-C所示
一种大棚蔬菜处在0℃以下的气温条件下超过3h,就会遭受冻害,秋末某天,该地区气象台发布如下的降温预报:由0时至次曰8时,气温y(℃)与时刻x(h)的函数关系如图中折线A-B-C所示查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com