
����Ŀ�����һ���������ܱ�һ���߶ηָ���������������Σ���ô�������߶�Ϊ��������ε������ߣ������������Ϊ���������Σ�
��1����ͼ1����ABC�ǵ�����������Σ�AB=AC(![]() )������ABC�Ľ�ƽ����BD��AC�ڵ�D����BD����ABC��һ�������ߣ�����BDC=______�ȣ�
)������ABC�Ľ�ƽ����BD��AC�ڵ�D����BD����ABC��һ�������ߣ�����BDC=______�ȣ�
��2����ͼ2����ABC�У���B=2��C���߶�AC�Ĵ�ֱƽ���߽�AC�ڵ�D����BC�ڵ�E����֤��AE����ABC��һ�������ߣ�
��3����ͼ3����֪��ABC�����������Σ�����A=30������BΪ�۽ǣ�������п��ܵ���B�Ķ�����������Ҫ�����ڴ����Ӧλ�����⻭ͼ����

���𰸡���1��72�� ��2��֤������������3��135���112.5���140�㣮
�������������������1��ֻҪ֤����ABE����AEC�ǵ��������μ��ɣ���2����ͼ2�У���BD��������ʱ���������������ۣ���ͼ3�У���AD��������ʱ��AB=BD��AD=DC���ݵ������������ʼ��ɽ�����⣬��CDΪ������ʱ���������⣮
�����������1��֤������ͼ1�У�
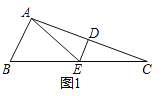
��DE���߶�AC�Ĵ�ֱƽ���ߣ�
��EA=EC������EAC�ǵ���������
���EAC=��C��
���AEB=��EAC+��C=2��C��
�ߡ�B=2��C��
���AEB=��B������EAB�ǵ��������Σ�
��AE����ABC��һ�������ߣ�
��2����ͼ2����

��BD��������ʱ�����AB=BD=DC������ABC=��ABD+��DBC=120��=15��=135����
���AD=AB��DB=DC������ABC=��ABD+��DBC=75��+37.5��=112.5����
���AD=DB��DC=CB������ABC=��ABD+��DBC=30��+60��=90��������������������
��ͼ3�У���AD��������ʱ��AB=BD��AD=DC������ABC=180��-20��-20��=140��
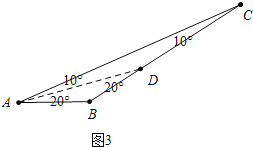
��CDΪ������ʱ���������⣮
��������������ABC�Ķ���Ϊ135����112.5����140����


 ״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д�
״Ԫ��ȫ��ͻ�Ƶ�����ϵ�д� ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
ֱͨ������У�ܲ��¿�ֱͨ��Уϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ��ÿ��С�����dz�Ϊ1����λ�������Σ���ѧУλ�õ�����ΪA(1��2)������������⣺
(1)����ͼ�н����ʵ���ֱ������ϵ����д��ͼ���Bλ�õ����ꣻ
(2)��������λ�õ�����ΪC(��3��3)����������ϵ�б�������ݵ�λ�ã���˳������ѧУ��ͼ��ݡ������ݣ��õ���ABC�����ABC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ��ͼ����
��ͼ����![]() �ύ��
�ύ��![]() ��
��![]() ���㣬��
���㣬��![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() ������Ϊ
������Ϊ![]() ���ҵ�
���ҵ�![]() ��
��![]() ʱ���κ����ĺ���ֵ
ʱ���κ����ĺ���ֵ![]() ��ȣ�
��ȣ�
��![]() ����ʵ��
����ʵ��![]() ��
��![]() ��ֵ��
��ֵ��
��![]() ����ͼ
����ͼ![]() ������
������![]() ��
��![]() ͬʱ��
ͬʱ��![]() ����������е�
����������е�![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ���
����λ���ȵ��ٶ���![]() �����յ�
�����յ�![]() �˶�����
�˶�����![]() ��ÿ��
��ÿ��![]() ����λ���ȵ��ٶ�������
����λ���ȵ��ٶ�������![]() �����˶�������
�����˶�������![]() ֹͣ�˶�ʱ����
ֹͣ�˶�ʱ����![]() ��ֹ֮ͣ�˶������˶�ʱ��Ϊ
��ֹ֮ͣ�˶������˶�ʱ��Ϊ![]() �룮����
�룮����![]() ����
����![]() ��
��![]() ���ۣ�ʹ��
���ۣ�ʹ��![]() ���ڵ�
���ڵ�![]() �����õ�
�����õ�![]() ��
��
���Ƿ����ijһʱ��![]() ��ʹ��
��ʹ��![]() Ϊֱ��������?�����ڣ����
Ϊֱ��������?�����ڣ����![]() ��ֵ���������ڣ���˵�����ɣ�
��ֵ���������ڣ���˵�����ɣ�
����![]() ��
��![]() �ص����ֵ����Ϊ
�ص����ֵ����Ϊ![]() ����
����![]() ����
����![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪����672����д��6��102+7��10+2�����ڶ���ʽ���ԣ�����ijһ��ĸ�Ķ���ʽ�����������ĸ�Ľ������б���7x+2+6x2����д��6x2+7x+2���ڽ������ʽ���������ʱ������ͨ���Աȷ��֣�������ȶ�λ���ij���������ʽ���м��㣬���磺��7x+2+6x2������2x+1��������672��21������ͼ����ˣ���7x+2+6x2������2x+1����3x+2�������Ķ����ϣ�

��1�����жϣ�x3��x2��5x��3�ܷ�x+1����_____��������������������������գ�
��2������ʽ2x5+3x3+5x2��2x+10����x2+1����ʽ��_____����ʽ��_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ȱ�������![]() �ı߳�Ϊ
�ı߳�Ϊ![]() �������������ͼ��ʾ��ƽ��ֱ������ϵ�У�����
�������������ͼ��ʾ��ƽ��ֱ������ϵ�У�����![]() ����
����![]() ���ϣ�
���ϣ�![]() �ߵĸ�
�ߵĸ�![]() ��
��![]() ���ϣ�һֻ���ӳ��
���ϣ�һֻ���ӳ��![]() ����������
����������![]() �ᵽ��
�ᵽ��![]() �㣬����
�㣬����![]() ����
����![]() �㣬��֪���ӳ���
�㣬��֪���ӳ���![]() �����˶����ٶ�����
�����˶����ٶ�����![]() ���˶��ٶȵ�
���˶��ٶȵ�![]() ���������ӳ�����ȫ�̵�ʱ����̣����
���������ӳ�����ȫ�̵�ʱ����̣����![]() ������Ϊ________��
������Ϊ________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ���ı���ABCD�Ķ���A��
���ı���ABCD�Ķ���A��![]() ���ڲ���B��C������OM�ϣ�C��B��O֮�䣩����
���ڲ���B��C������OM�ϣ�C��B��O֮�䣩����![]() ����D��ON�ϣ�����CD��OMʱ���ı���ABCD���ܳ���С�����ʱAD�ij�����__________��
����D��ON�ϣ�����CD��OMʱ���ı���ABCD���ܳ���С�����ʱAD�ij�����__________��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������У��Ǽ�������ǣ�������
A.����ABC�У�����B����C����A������ABC��ֱ��������
B.����ABC�У���a![]() ����b+c�� ��b��c��������ABC��ֱ��������
����b+c�� ��b��c��������ABC��ֱ��������
C.����ABC�У�����A����B����C��3��4��5������ABC��ֱ��������
D.����ABC�У���a��b��c��3��4��5������ABC��ֱ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=x�뷴��������y=![]() ��k��0����ͼ���ڵ�һ�����ڽ��ڵ�A��2��m����
��k��0����ͼ���ڵ�һ�����ڽ��ڵ�A��2��m����
��1����m��k��ֵ��
��2����B��y�Ḻ�����ϣ�����AOB�����Ϊ2����AB����ֱ�ߵĺ�������ʽ��
��3������AOB��ֱ��AB����ƽ�ƣ�ƽ�ƺ�A��O��B�Ķ�Ӧ��ֱ�ΪA'��O'��B'������O'ǡ�����ڷ���������y=![]() ��ͼ����ʱ�����A'�����꣮
��ͼ����ʱ�����A'�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() �У�
�У�![]() ���ף�
���ף�![]() ���ף���
���ף���![]() ��
��![]() ��������ÿ��
��������ÿ��![]() �����ٶ���
�����ٶ���![]() �˶�����
�˶�����![]() ��
��![]() ͬʱ��������ÿ��
ͬʱ��������ÿ��![]() �����ٶ���
�����ٶ���![]() �˶�������һ�����㵽�˵�ʱ����һ������Ҳ��Ӧֹͣ�˶�����ô������
�˶�������һ�����㵽�˵�ʱ����һ������Ҳ��Ӧֹͣ�˶�����ô������![]() ��
��![]() ��
��![]() �������������
Ϊ�������������![]() ����ʱ���˶�ʱ��Ϊ________��
����ʱ���˶�ʱ��Ϊ________��

�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com