
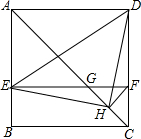
 如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )
如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论中结论正确的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 ①根据题意可知∠ACD=45°,则GF=FC,则EG=EF-GF=CD-FC=DF;
②由SAS证明△EHF≌△DHC,得到∠HEF=∠HDC,从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=180°;
③同②证明△EHF≌△DHC即可;
④若$\frac{AE}{AB}=\frac{2}{3}$,则AE=2BE,可以证明△EGH≌△DFH,得△EHD为等腰直角三角形,设HM=x,则CF=2x,DF=2FC=4x,分别表示S△CFH=$\frac{1}{2}$×HM×CF=$\frac{1}{2}$•x•2x=x2,S△EDH=$\frac{1}{2}$×DH2=$\frac{1}{2}$×$(\sqrt{26}x)^{2}$=13x2,可得结论.
解答 解:①∵四边形ABCD为正方形,EF∥AD,
∴EF=AD=CD,∠ACD=45°,∠GFC=90°,
∴△CFG为等腰直角三角形,
∴GF=FC,
∵EG=EF-GF,DF=CD-FC,
∴EG=DF,
故①正确;
②∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH=$\frac{1}{2}$∠GFC=45°=∠HCD,
在△EHF和△DHC中,
$\left\{\begin{array}{l}{EF=CD}\\{∠EFH=∠DCH}\\{FH=CH}\end{array}\right.$,
∴△EHF≌△DHC(SAS),
∴∠HEF=∠HDC,
∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=∠AEF+∠ADF=180°,
故②正确;
③由②知:△EHF≌△DHC,
故③正确;
④∵$\frac{AE}{AB}$=$\frac{2}{3}$,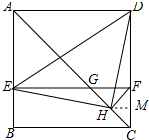
∴AE=2BE,
∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=GH,∠FHG=90°,
∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD,
在△EGH和△DFH中,
$\left\{\begin{array}{l}{EG=DF}\\{∠EGH=∠HFD}\\{GH=FH}\end{array}\right.$,
∴△EGH≌△DFH(SAS),
∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,
∴△EHD为等腰直角三角形,
过H点作HM垂直于CD于M点,如图所示:
设HM=x,则CF=2x,
∴DF=2FC=4x,
∴DM=5x,DH=$\sqrt{26}$x,CD=6x,
则S△CFH=$\frac{1}{2}$×HM×CF=$\frac{1}{2}$•x•2x=x2,S△EDH=$\frac{1}{2}$×DH2=$\frac{1}{2}$×$(\sqrt{26}x)^{2}$=13x2,
∴则S△EDH=13S△CFH,故④正确;
其中结论正确的有:①②③④,4个;
故选D.
点评 本题考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、勾股定理、三角形面积的计算等知识;熟练掌握正方形的性质,证明三角形全等是解决问题的关键,本题虽然是选择题,但相当于四个证明题,比较麻烦,要细心研究,依次解决.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是( )
如图是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是( )| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
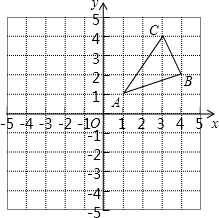 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com