
【题目】如图,平面直角坐标系xoy中,抛物线y=a(x+1)(x-9)经过A,B两点,四边形OABC
矩形,已知点A坐标为(0,6)。

(1) 求抛物线解析式;
(2) 点E在线段AC上移动(不与C重合),过点E作EF⊥BE,交x轴于点F.请判断![]() 的值是否变化;若不变,求出它的值;若变化,请说明理由。
的值是否变化;若不变,求出它的值;若变化,请说明理由。
(3)在(2)的条件下,若E在直线AC上移动,当点E关于直线BF的对称点![]() 在抛物线对称轴上时,请求出BE的长度。
在抛物线对称轴上时,请求出BE的长度。
【答案】(1)![]() (2)不变 (3)
(2)不变 (3)![]()
【解析】分析(1) 将![]() 代入
代入![]() 即可求解;(2)由△BDE∽△EGF,得出
即可求解;(2)由△BDE∽△EGF,得出![]() ,由点A的坐标及对称轴直线x=4推出点B坐标,从而求解;(3) 过点E′作PQ∥x,易证△FPE′∽△BQE′,得出FP=3,利用CQ=3, BQ=9,求出BE即可得出结果.
,由点A的坐标及对称轴直线x=4推出点B坐标,从而求解;(3) 过点E′作PQ∥x,易证△FPE′∽△BQE′,得出FP=3,利用CQ=3, BQ=9,求出BE即可得出结果.
(1)将![]() 代入
代入![]() ,得:
,得:![]()
∴抛物线解析式为![]()
(2)![]() 的值不变.
的值不变.
如图,过点E作DG⊥AB交AB于点D,交![]() 轴于点G
轴于点G

∵四边形OABC为矩形, ∴DG⊥OC , BD=GC
由BE⊥EF, 易证△BDE∽△EGF, 得:![]() , 即
, 即![]() .
.
由![]() ,抛物线对称轴为直线
,抛物线对称轴为直线![]() ,得
,得![]() , 即OC=6.
, 即OC=6.
易知![]() , ∴
, ∴![]() .
.
(3)如图,过点E′作PQ∥x,FP⊥PQ, CQ⊥PQ.

易证△FPE′∽△BQE′.
可知QE′=4, ∴FP=3. 则CQ=3, BQ=9
∴BE=BE′=![]() .
.


 优学名师名题系列答案
优学名师名题系列答案科目:初中数学 来源: 题型:
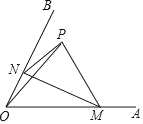
【题目】如图,∠AOB=60°,点P是∠AOB内的定点且OP=![]() ,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是( )
A. ![]() B.
B. ![]() C. 6 D. 3
C. 6 D. 3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知A=3a2b﹣2ab2+abc,B=﹣2a2b+ab2+2abc.
(1)求2A﹣B;
(2)小强同学说:“当c=﹣2018时和c=2018时,(1)中的结果都是一样的”,你认为对吗?说明理由;
(3)若a=![]() ,b=
,b=![]() ,求2A﹣B的值.
,求2A﹣B的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
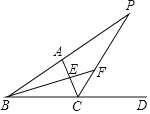
【题目】如图,已知BE是△ABC的角平分线,CP是△ABC的外角∠ACD的平分线.延长BE,BA分别交CP于点F,P.
(1)求证:∠BFC![]() ∠BAC;
∠BAC;
(2)小智同学探究后提出等式:∠BAC=∠ABC+∠P.请通过推理演算判断“小智发现”是否正确?
(3)若2∠BEC﹣∠P=180°,求∠ACB的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于平面直角坐标系xOy中的任意两点M(x1,y1),N(x2,y2),给出如下定义:
将|x1﹣x2|称为点M,N之间的“横长”,|y1﹣y2|称为点M,N之间的纵长”,点M与点N的“横长”与“纵长”之和称为“折线距离”,记作d(M,N)=|x1﹣x2|+|y1﹣y2|“.
例如:若点M(﹣1,1),点N(2,﹣2),则点M与点N的“折线距离”为:d(M,N)=|﹣1﹣2|+|1﹣(﹣2)|=3+3=6.
根据以上定义,解决下列问题:
已知点P(3,2).
(1)若点A(a,2),且d(P,A)=5,求a的值;
(2)已知点B(b,b),且d(P,B)<3,直接写出b的取值范围;
(3)若第一象限内的点T与点P的“横长”与“纵长”相等,且d(P,T)>5,简要分析点T的横坐标t的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列一元一次方程解应用题
为发展校园足球运动,某区四校决定联合购买![]() 套队服和
套队服和![]() (
(![]() 且为整数)个足球,市场调查发现:甲、乙两商城以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多
且为整数)个足球,市场调查发现:甲、乙两商城以同样的价格出售同种品牌的足球队服和足球,已知每套队服比每个足球多![]() 元,两套队服与三个足球的费用相等.经洽谈,甲商城优惠方案是:每购买十套队服,送一个足球;乙商城优惠方案是:若购买队服超过
元,两套队服与三个足球的费用相等.经洽谈,甲商城优惠方案是:每购买十套队服,送一个足球;乙商城优惠方案是:若购买队服超过![]() 套,则购买足球打八折
套,则购买足球打八折
(1)求每套队服和每个足球的价格是多少?
(2)请用含![]() 的式子分别表示出甲商城所花的费用___________元;乙商城购买装备所花的费用___________元
的式子分别表示出甲商城所花的费用___________元;乙商城购买装备所花的费用___________元
(3)求出到甲、乙两家购买所需花的费用相同时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校在一次环保知识宣传活动中,需要印刷若干份调查问卷。印刷厂有甲、乙两种收费方式:甲种方式收制版费6元,每一份收印刷费0.1元;乙种方式不收制版费,每印一份收印刷费0.12元。设共印调查问卷![]() 份:
份:
(1)按甲种方式应收费多少元,按乙种方式应收费多少元(用含![]() 的代数式表示);
的代数式表示);
(2)若共需印刷500份调查问卷,通过计算说明选用哪种方式合算?
(3)印刷多少份调查问卷时,甲、乙两种方式收费一样多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com