
【题目】万圣节两周前,某商店购进1000个万圣节面具,进价为每个6元,第一周以每个10元的价格售出200个;随着万圣节的临近,预计第二周若按每个10元的价格销售可售出400个,但商店为了尽快减少库存,决定单价降价x元销售![]() 根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价
根据市场调查,单价每降低1元,可多售出100个,但售价不得低于进价![]() ;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
;节后,商店对剩余面具清仓处理,以第一周售价的四折全部售出.
![]() 当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
当单价降低2元时,计算第二周的销售量和售完这批面具的总利润;
![]() 如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
如果销售完这批面具共获利1300元,问第二周每个面具的销售价格为多少元?
【答案】(1)当单价降低2元时,第二周的销售量为600和售完这批面具的总利润1600 ;(2) 第二周的销售价格为![]() 元.
元.
【解析】
(1)第二周的销售量=400+100x.利润=售价-成本价;
(2)根据纪念品的进价和售价以及销量分别表示出两周的总利润,进而得出等式求出即可.
(1)第二周的销售量为:400+100x=400+100x=400+100×2=600.
总利润为:200×(10-6)+(8-6)×600+200(4-6)=1600.
答:当单价降低2元时,第二周的销售量为600和售完这批面具的总利润1600;
![]() 由题意得出:200×(10-6)+(10-x-6)(400+100x)+(4-6)[(1000-200)-(400+100x)]=1300,
由题意得出:200×(10-6)+(10-x-6)(400+100x)+(4-6)[(1000-200)-(400+100x)]=1300,
整理得:x2-2x-3=0,
解得:x1=3;x2=-1(舍去),
∴10-3=7(元).
答:第二周的销售价格为7元.


 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案科目:初中数学 来源: 题型:
【题目】已知,如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边三角形ABC和等边三角形CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连结PQ,OC,以下四个结论:①AD=BE;②三角形CPQ是等边三角形;③AD⊥BC;④OC平分∠AOE其中正确的结论有______(把你认为正确的序号都填上).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,D、E分别是AB、AC的中点,连接CD,过E作EF∥DC交BC的延长线于F.
(1)证明:四边形CDEF是平行四边形;
(2)若四边形CDEF的周长是25cm,AC的长为5cm,求线段AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() .
.
![]() 求证:方程有两个实数根;
求证:方程有两个实数根;
![]() 若
若![]() 的两边AB,AC的长是这个方程的两个实数根
的两边AB,AC的长是这个方程的两个实数根![]() 第三边BC的长为3,当
第三边BC的长为3,当![]() 是等腰三角形时,求k的值.
是等腰三角形时,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】苏果超市用5000元购进一批新品种的苹果进行试销,由于试销状况良好,超市又调拨11000元资金购进该种苹果,但这次的进价比试销时每千克多了0.5元,购进苹果的数量是试销时的2倍。
(1)试销时该品种苹果的进价是每千克多少元?
(2)如果超市将该品种的苹果按每千克7元定价出售,当大部分苹果售出后,余下的400千克按定价的七折售完,那么超市在这两次苹果销售中共盈利多少元?(7分)
查看答案和解析>>
科目:初中数学 来源: 题型:
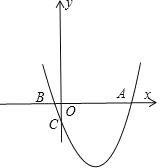
【题目】在直角坐标平面内,点 O 为坐标原点,二次函数 y=x2+(k﹣5)x﹣(k+4)的图象交 x 轴于点 A(x1,0)、B(x2,0),且 x1>x2,x1x2+(x1+x2)+1=8.
(1)求二次函数的解析式;
(2)设函数的图象与 y 轴的交点为点 C,求△AOC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某星期天,八(1)班开展社会实践活动,第一小组花90元从蔬菜批发市场批发了黄瓜和茄子共40kg,到蔬菜市场去卖,黄瓜和茄子当天的批发价与零售价如表所示:
品名 | 黄瓜 | 茄子 |
批发价/(元/kg) | 2.4 | 2 |
零售价/(元/kg) | 3.6 | 2.8 |
(1)黄瓜和茄子各批发了多少kg?
(2)该小组当天卖完这些黄瓜和茄子可赚多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于点A,B,与
与x轴交于点A,B,与![]() 轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。
轴交于点C。过点C作CD∥x轴,交抛物线的对称轴于点D,连结BD。已知点A坐标为(-1,0)。

(1)求该抛物线的解析式;
(2)求梯形COBD的面积。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com