
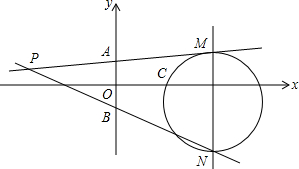
 如图,在平面直角坐标系xOy中,已知点A(0,1),B(0,-1).点P是平面内任意一点,直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆恰好经过点C(2,0),则称此时的点P为理想点.
如图,在平面直角坐标系xOy中,已知点A(0,1),B(0,-1).点P是平面内任意一点,直线PA,PB与直线x=4分别交于M,N两点.若以MN为直径的圆恰好经过点C(2,0),则称此时的点P为理想点.分析 (1))①如图1中,O′是MN的中点,由△P1AB∽△P1MN得$\frac{AB}{MN}$=$\frac{{P}_{1}0}{{P}_{1}O′}$,求出MN,即可判断.
②如图2,画出图形即可判断点P2不是理想点.
(2)存在,如图3中,作PK⊥MN由H,交AB于G,假设P是理想点,MN与x轴的交点为H,由AB∥MN,得△PAB∽△PMN,得$\frac{AB}{MN}$=$\frac{PG}{PK}$,求出MN,得到点M的坐标,再求出直线AM的解析式,即可求出点P坐标,再根据对称性求得另一个理想点.
(3)如图4中,假设点P在x轴的正半轴上,是理想点,求出点P坐标即可解决问题.
解答 解:(1)①如图1中,O′是MN的中点,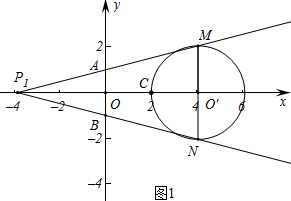
∵AB∥MN,
∴△P1AB∽△P1MN,
∴$\frac{AB}{MN}$=$\frac{{P}_{1}0}{{P}_{1}O′}$,
∴$\frac{2}{MN}$=$\frac{2}{4}$,
∴MN=2,
∴O′M=O′N=2,
∵CO′=2,
∴点C在⊙O′上,
∴点P1是理想点.
②由图2可知,点P2不是理想点.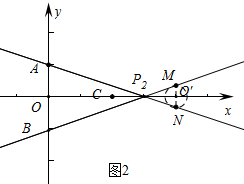
(2)存在,
如图3中,作PK⊥MN由H,交AB于G,假设P是理想点,MN与x轴的交点为H.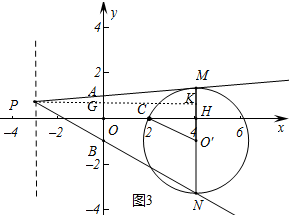
∵AB∥MN,
∴△PAB∽△PMN,
∴$\frac{AB}{MN}$=$\frac{PG}{PK}$,
∴$\frac{2}{MN}$=$\frac{3}{7}$,
∴MN=$\frac{14}{3}$,
∴O′M=$\frac{7}{3}$,
在RT△CHO′中,O′H=$\sqrt{CO{′}^{2}-C{H}^{2}}$=$\frac{\sqrt{13}}{3}$,
∴MH=$\frac{7}{3}$-$\frac{\sqrt{13}}{3}$=$\frac{7-\sqrt{13}}{3}$,
∴点M坐标(4,$\frac{7-\sqrt{13}}{3}$),
∴直线AM的解析式为y=$\frac{4-\sqrt{13}}{12}$x+1,
∴x=-3时,y=$\frac{\sqrt{13}}{4}$,
∴点P坐标(-4,$\frac{\sqrt{13}}{4}$),
根据对称性点P′(-4,-$\frac{\sqrt{13}}{4}$)也是理想点.
线x=-3上存在理想点,理想点的纵坐标为±$\frac{\sqrt{13}}{4}$.
(3)如图4中,假设点P在x轴的正半轴上,是理想点.
∵AB∥MN,AB=2,MN=4,
∴△PAB∽△PNM,
∴$\frac{AB}{MN}$=$\frac{PO}{PO′}$,
∴$\frac{2}{4}$=$\frac{PO}{4-PO}$,
∴PO=$\frac{4}{3}$,
∴点P坐标($\frac{4}{3}$,0),
∵点P1(-4,0)也是理想点,由图象可知,
若动直线x=m(m≠0)上存在理想点,则m的取值范围是-4≤m<0或0<m≤$\frac{4}{3}$.
点评 本题考查圆的综合题、点与圆的位置关系、一次函数、相似三角形的判定和性质等知识,解题的关键是理解题意,学会正确画出图形,学会利用相似三角形性质解决问题,属于中考压轴题,属于创新性题目.


 阶梯计算系列答案
阶梯计算系列答案科目:初中数学 来源: 题型:选择题
| A. | x1=-1,x2=1 | B. | x1=-1,x2=2 | C. | x1=-2,x2=1 | D. | x1=-2,x2=2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
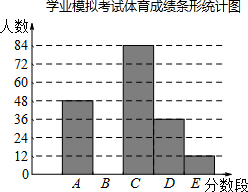 为迎接2016年贵阳市初中毕业生学业体育考试,某校进行了九年级学生学业考试体育模拟考试.为了解本次模拟考试的成绩(分数为整数)情况,现从中随机抽取部分学生的体育成绩分为五个等级,其中A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分.根据所分等级情况制作了如下两个不完整的统计图表:
为迎接2016年贵阳市初中毕业生学业体育考试,某校进行了九年级学生学业考试体育模拟考试.为了解本次模拟考试的成绩(分数为整数)情况,现从中随机抽取部分学生的体育成绩分为五个等级,其中A:50分;B:49-45分;C:44-40分;D:39-30分;E:29-0分.根据所分等级情况制作了如下两个不完整的统计图表:| 分数段 | 人数/人 | 频数 |
| A | 48 | 0.2 |
| B | m | 0.25 |
| C | 84 | 0.35 |
| D | 36 | n |
| E | 12 | 0.05 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
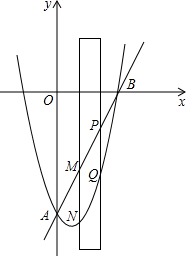 如图,抛物线与直线y=2x-8交于A,B两点,有一直尺平行于y轴移动,直尺两长边所在直线AB和抛物线截得两线段NM、PQ,点P、M在直线AB上且PM=$\sqrt{5}$,设M点的横坐标为m(0<m<4).
如图,抛物线与直线y=2x-8交于A,B两点,有一直尺平行于y轴移动,直尺两长边所在直线AB和抛物线截得两线段NM、PQ,点P、M在直线AB上且PM=$\sqrt{5}$,设M点的横坐标为m(0<m<4).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | “抛掷一枚硬币,正面向上”是不可能事件 | |
| B. | 一组数据2,3,4,5,5,2,4,2,2的中位数是3 | |
| C. | 若甲、乙两组数据的方差分别为S甲2=1.2、S乙2=2.3,则乙组数据比甲组数据稳定 | |
| D. | 掷一枚骰子,偶数点向上的概率为$\frac{1}{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com