练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    20．某市由于周边蔬菜产地的蔬菜减产，菜价一路上涨，其中四季豆价格比原来上涨1倍，某饭店同样用60元钱却比原来少买四季豆50斤，你能求出原来每斤四季豆的价格吗？请分析题中的等量关系，并列出符合题意的方程．（“斤”是传统质量单位，2斤=1千克）

    分析 设原来每斤四季豆的价格是x元，根据购买数量=$\frac{金额}{单价}$和用60元钱却比原来少买四季豆50斤列出方程并解答．

    解答 解：设原来每斤四季豆的价格是x元，
    依题意得：$\frac{60}{x}$-$\frac{60}{2x}$=50，
    解得x=0.6．
    经检验：x=0.6是所列方程的解，且符合题意．
    答：原来每斤四季豆的价格是0.6元．

    点评 本题考查分式方程的应用，分析题意，找到关键描述语，找到合适的等量关系是解决问题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

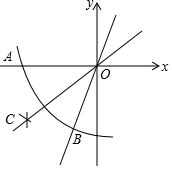    19．如图，在平面直角坐标系中，依下列步骤尺规作图，并保留作图痕迹：
    步骤1：以点O为圆心，任意长为半径画弧，与x轴负半轴交于点A，与直线y=$\sqrt{3}$x交于点B（点B在第三象限）：
    步骤2：分别以点A，B为圆心，以大于$\frac{1}{2}$AB长为半径画弧，两弧交于点C．
    则直线OC的函数解析式为（　　）
    A．y=$\frac{\sqrt{3}}{2}$xB．y=-$\frac{\sqrt{3}}{2}$xC．y=$\frac{\sqrt{3}}{3}$xD．y=-$\frac{\sqrt{3}}{3}$x

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．我区注重城市绿化提高市民生活质量，新建林荫公园计划购买甲、乙两种树苗共800株，甲种树苗每株12元，乙种树苗每株15元．相关资料表明：甲、乙两种树苗的成活率分别为85%、90%．
    （1）若购买这两种树苗共用去10500元，则甲、乙两种树苗各购买多少株？
    （2）若要使这批树苗的总成活率不低于88%，则甲种树苗至多购买多少株？
    （3）在（2）的条件下，应如何选购树苗，使购买树苗的费用最低？并求出最低费用．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    8．如图，一透明的圆柱体玻璃杯，从内部测得底部直径为6cm，杯深8cm．今有一根长为16cm的吸管如图放入杯中，露在杯口外的长度为h，则h的变化范围是：6cm≤h≤8cm．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    15．如图，在△ABC中，∠ACB=85°，DE过点C，且DE∥AB，若∠ACD=55°，则∠B的度数是40°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    5．观察下列各式：
    $\frac{{1}^{2}+1-1}{{1}^{2}+1}$=1-$\frac{1}{{1}^{2}+1}$=1-（1-$\frac{1}{2}$）；
    $\frac{{2}^{2}+2-1}{{2}^{2}+2}$=1-$\frac{1}{{2}^{2}+2}$=1-（$\frac{1}{2}$-$\frac{1}{3}$）；
    $\frac{{3}^{2}+3-1}{{3}^{2}+3}$=1-$\frac{1}{{3}^{2}+3}$=1-（$\frac{1}{3}$-$\frac{1}{4}$）；
    …
    计算：$\frac{1}{2}$+$\frac{5}{{2}^{2}+2}$+$\frac{11}{{3}^{2}+3}$+…+$\frac{201{5}^{2}+2015-1}{201{5}^{2}+2015}$=2014$\frac{1}{2016}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．为了维护安全舒适的乘机环境，防止易燃易爆物品危及他人安全，民航要求乘坐飞机的旅客必须接受安检，重庆江北国际机场开设有10个安检通道，现有门式安检和手持式安检两种方式，每个门式安检需要3名工作人员，每分钟可检查10人，每只手持式安检需要1名工作人员，每分钟可检查2人，每条通道可安放一台门式安检仪或一只手持式安检仪，每分钟到达安检口的总人数为80人．
    （1）若要保证一分钟内（不考虑上一分钟的累积）所有安检口等候安检的人数不超过20人，则至少需要开设多少个门式安检仪？
    （2）随着节假日的来临，每分钟到达安检口旅客人数增加了1.3a，为了确保旅客尽快通过安检，机场打算升级安检门设备，每分钟通过安检人数比原来提高了2a%，安放门式安检仪数量比（1）条件下的最少值增加a%，而手持式安检仪每分钟安检人数不变，在总的安检通道不变的情况下，每分钟到达的旅客恰好能全部通过安检，求a的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．感知：如图①，OC平分∠AOB，P是OC上任意一点，PM⊥OA于点M，PN⊥OB于点N，由三角形全等的判定方法“AAS”易证△OPM≌△OPN，得到角平分线的一条性质“角平分线上的点到这个角两边的距离相等”．
    探究：如图②，在平面直角坐标系中，已知A（7，0），B（7，24），点D在线段AB上，OD平分∠AOB，求$\frac{AD}{OA}$的值．
    应用：将图②中的∠AOB绕原点O顺时针旋转，使∠AOB的边OB落在第一象限的角平分线上，如图③，点P在∠AOB的平分线上，当点P的横、纵坐标均为整数时，OP长度的最小值为5$\sqrt{2}$．（可参考提供的网格求值）

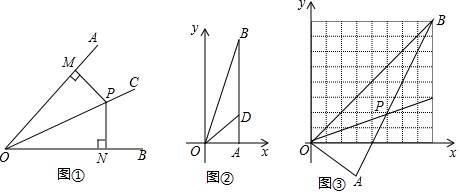
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    10．下列运算正确的是（　　）
    A．$\sqrt{18}$-$\sqrt{8}$=$\sqrt{10}$B．（-3xy）2=6x2y2C．（-21）0=1D．a6÷a2=a3

    查看答案和解析>>

    同步练习册答案