
���� ��1���������ҵ��������Ҫx�죬���ݵ�����ϵ���ҵĹ���Ч�ʡ�10��+���Һ����Ĺ���Ч�ʡ�14��=1�ɵ÷�ʽ���̣��ⷽ�̿ɵô𰸣�
��2������̶�����Ҫ����ʩ��a�����ʣ������ǣ�1-$\frac{1}{45}$a�������Ӻ�����Ҫ�������ǣ�$\frac{1-\frac{1}{45}a}{\frac{1}{30}+\frac{1}{45}}$����������ɵò��ȹ�ϵ���ҵ����ɵ�������0.6��Ԫ+���Ӻ�������������1+0.6����Ԫ��28��Ԫ���ɴ��г�����ʽ���ⲻ��ʽ���ɣ�
��� �⣺��1�����������Ҷӵ�������������Ҫx�죬������ã�
$\frac{10}{x}$+��$\frac{1}{x}$+$\frac{1}{30}$����14=1��
��ã�x=45��
�����飺x=45��ԭ��ʽ���̵Ľ⣬
�𣺰����Ҷӵ�������������Ҫ45�죻
��2�����Ҷ���a������ɼס������Ӻ�����ɴ���̣�
������ã�0.6��a+��1+0.6����$\frac{1-\frac{1}{45}a}{\frac{1}{30}+\frac{1}{45}}$����28��
��ã�a��20��
�𣺼��̶�����Ҫ����ʩ��20������ɼס������Ӻ���ʩ����ɴ�����ʣ�µĹ��̣�����ʹʩ�����ò�����28��Ԫ��
���� ������Ҫ�����˷�ʽ������һԪһ�β���ʽ��Ӧ�ã��ؼ�������Ū�����⣬�ҳ���Ŀ�еĵ�����ϵ�ȹ�ϵ���г����̻�ʽ�������õ��Ĺ�ʽ�ǣ�����Ч�ʡ�����ʱ��=��������


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��P���߶�AB�Ļƽ�ָ�㣬��AP��PB������APΪ�߳���������ACDP�����ΪS1����BF��AB�ij�Ϊ�ڱߵľ���AEFB�����ΪS2��BF=PB������S1��S2�кι�ϵ��
��ͼ����֪��P���߶�AB�Ļƽ�ָ�㣬��AP��PB������APΪ�߳���������ACDP�����ΪS1����BF��AB�ij�Ϊ�ڱߵľ���AEFB�����ΪS2��BF=PB������S1��S2�кι�ϵ���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a+b | B�� | a-b | C�� | $\frac{a+b}{a-b}$ | D�� | $\frac{a-b}{a+b}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
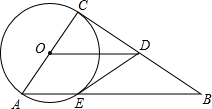 ��ͼ��Rt��ABC�У���C=90�㣬��ACΪֱ���ġ�O��б��AB��E��OD��AB����֤��
��ͼ��Rt��ABC�У���C=90�㣬��ACΪֱ���ġ�O��б��AB��E��OD��AB����֤���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x2+x4=x6 | B�� | ��-x3��2=x6 | C�� | 2a+3b=5ab | D�� | x6��x3=x2��x��0�� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com