
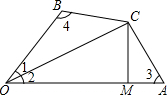
 如图,在四边形OACB中,CM⊥OA于M,∠1=∠2,CA=CB.求证:
如图,在四边形OACB中,CM⊥OA于M,∠1=∠2,CA=CB.求证:分析 首先过C作CE⊥OB于E,证明Rt△ECB≌Rt△MCA,进而得出Rt△ECO≌Rt△MCO,再利用全等三角形的性质得出结论即可.
解答 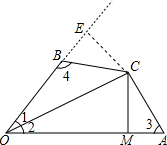 证明:作CE⊥OB于E,
证明:作CE⊥OB于E,
∵CM⊥OA,
∴∠CEB=∠CMA=90°,
又∵∠1=∠2,
∴CE=CM,
在Rt△ECB和Rt△MCA中,
$\left\{\begin{array}{l}{EC=MC}\\{CB=CA}\end{array}\right.$,
∴Rt△ECB≌Rt△MCA(HL),
∴∠3=∠EBC,BE=AM,
在Rt△ECO和Rt△MCO中,
$\left\{\begin{array}{l}{CO=CO\\;}\\{EC=CM}\end{array}\right.$,
∴Rt△ECO≌Rt△MCO(HL),
∴EO=OM,
∵∠EBC+∠4=180°,
∴∠3+∠4=180°;
∴OA+OB=OM+AM+BO=OM+EB+BO=2OM.
点评 此题主要考查了全等三角形的判定与性质以及角平分线的性质等知识,熟练掌握全等三角形的判定是解题关键.


科目:初中数学 来源: 题型:解答题
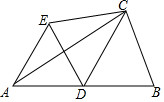 如图,在△ABC中,CD是AB边的中线,∠CDB=60°,将△BCD沿CD折叠,使点B落在点E的位置.
如图,在△ABC中,CD是AB边的中线,∠CDB=60°,将△BCD沿CD折叠,使点B落在点E的位置.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,D、E分别是△ABC两边AB、AC上的点,试问在下列条件下△ADE与△ACB是否相似,并说明理由.
已知:如图,D、E分别是△ABC两边AB、AC上的点,试问在下列条件下△ADE与△ACB是否相似,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com