练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
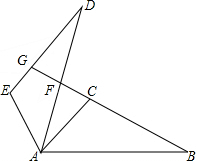
    4．如图所示，△ABC≌△ADE，且∠CAD=10°，∠D=25°，∠EAB=120°，求∠DFB的度数．

    分析 根据△ABC≌△ADE、∠D=25°，即可得出∠B=∠D=25°、∠EAD=∠CAB，再根据∠EAB=120°、∠CAD=10°通过角的计算可得出∠FAB=65°，由外角的性质即可得出∠DFB的度数，此题得解．

    解答 解：∵△ABC≌△ADE，∠D=25°，
    ∴∠B=∠D=25°，∠EAD=∠CAB．
    ∵∠EAB=∠EAD+∠CAD+∠CAB=120°，∠CAD=10°，
    ∴∠CAB=（120°-10°）÷2=55°，
    ∴∠FAB=∠CAB+∠CAD=55°+10°=65°．
    又∵∠DFB是△ABF的外角，
    ∴∠DFB=∠B+∠FAB，
    ∴∠DFB=25°+65°=90°．

    点评 本题考查了全等三角形的性质以及外角的性质，熟练掌握全等三角形的性质是解题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    3．如图1，已知∠PMN=90°，⊙O与PM切于点C，与MN交于B，D两点，延长BO交⊙O于A．
    （1）求证：$\widehat{AC}$=$\widehat{DC}$；
    （2）如图2，若MD=8，BD=3MB，E为$\widehat{AD}$的中点，求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    15．列方程解应用题．
    某单位组织员工去天水湾风景区旅游，共支付给旅行社27000元．如果人数不超过25人，人均旅游费用为1000元，如果人数超过25人，每增加1人，人均旅游费用降低20元．但人均旅游费用不得低于700元．请问该单位这次共有多少名员工去天水湾风景区旅游？

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．我们定义一种新运算：a*b=a2-b+ab．例如：1*3=12-2+1×2=1
    （1）求2*（-3）的值．
    （2）求（-2）*[2*（-3）]的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    19．计算
    （1）（-1$\frac{3}{4}$）-（+6$\frac{1}{3}$）-2.25+$\frac{10}{3}$ 
    （2）-9×（-11）-3÷（-3）
    （3）8×（-$\frac{2}{5}$）-（-4）×（-$\frac{2}{9}$）+（-8）×$\frac{3}{5}$  
    （4 ）（$\frac{1}{2}$+$\frac{5}{6}$-$\frac{7}{12}$）÷（-$\frac{1}{24}$）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    9．如图1，BC是⊙O的直径，点A在⊙O上，AD⊥BC，垂足为D，$\widehat{AE}$=$\widehat{AB}$，BE分别交AD、AC于点F、G．
    （1）判断△FAG的形状，并说明理由；
    （2）如图2，若点E和点A在BC的两侧，BE、AC的延长线交于点G，AD的延长线交BE于点F，其余条件不变，（1）中的结论还成立吗？请说明理由；
    （3）在（2）的条件下，若BG=26，BD-DF=7，求AB的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    16．根据表格对应值：
    x3.243.253.26
    ax2+bx+c-1 13
    判断关于x的方程ax2+bx+c-2=0的一个解x的范围是（　　）
    A．x＜3.24B．3.24＜x＜3.25C．3.25＜x＜3.26D．3.26＜x

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

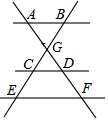    13．如图．AB∥CD∥EF，AF、BE交于点G，下列比例式错误的是（　　）
    A．$\frac{AD}{DF}=\frac{BC}{CE}$B．$\frac{AG}{GD}=\frac{BG}{CG}$C．$\frac{GC}{GE}=\frac{CD}{EF}$D．$\frac{AB}{EF}=\frac{AG}{GE}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．有一个坡角，坡度i=1：$\sqrt{3}$，则坡角α=30°．

    查看答案和解析>>

    同步练习册答案