
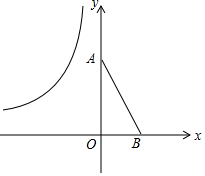
 如图,已知原点O,A(0,4),B(2,0),将△OAB绕平面内一点P逆时针旋转90°,使得旋转后的三角形的两个顶点恰好落在双曲线y=$\frac{-6}{x}$(x<0)上,则旋转中心P的坐标为(-$\frac{3}{2}$,-$\frac{1}{2}$).
如图,已知原点O,A(0,4),B(2,0),将△OAB绕平面内一点P逆时针旋转90°,使得旋转后的三角形的两个顶点恰好落在双曲线y=$\frac{-6}{x}$(x<0)上,则旋转中心P的坐标为(-$\frac{3}{2}$,-$\frac{1}{2}$). 分析 根据旋转的性质得:A′O′=AO=4,O′B′=OB=2,因为A′和B′恰好落在双曲线y=$\frac{-6}{x}$(x<0)上,设A′(m,-$\frac{6}{m}$),则B′(m+4,-$\frac{6}{m}$+2),根据反比例函数列式为:(m+4)(-$\frac{6}{m}$+2)=-6,求m的值,写出A′和B′的坐标,作辅助线,构建两全等三角形,根据A′G=PH,PG=AH,列方程组可得结论.
解答 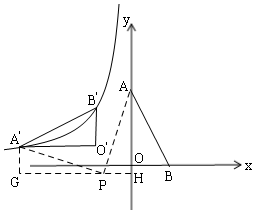 解:由旋转得:△AOB≌△A′O′B′,
解:由旋转得:△AOB≌△A′O′B′,
∴A′O′=AO=4,O′B′=OB=2,
设A′(m,-$\frac{6}{m}$),则B′(m+4,-$\frac{6}{m}$+2),
则(m+4)(-$\frac{6}{m}$+2)=-6,
m2+4m-12=0,
(m+6)(m-2)=0,
m1=-6,m2=2(舍),
∴A′(-6,1),B′(-2,3),
过P作GH∥x轴,交y轴于H,过A′作A′G⊥x轴,连接PA、PA′,
设P(x,y),
则A′G=1-y,PG=6+x,PH=-x,AH=4-y,
由旋转得:AP=A′P,
易证明△PA′G≌△APH,
∴A′G=PH,PG=AH,
则$\left\{\begin{array}{l}{1-y=-x}\\{6+x=4-y}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=-\frac{3}{2}}\\{y=-\frac{1}{2}}\end{array}\right.$,
∴P(-$\frac{3}{2}$,-$\frac{1}{2}$);
故答案为:(-$\frac{3}{2}$,-$\frac{1}{2}$).
点评 本题考查了反比例函数图象上点的特征、旋转的性质、三角形全等的性质和判定,本题画出图出旋转后的三角形确定点P的位置是关键,根据旋转角为直角构建全等三角形解决问题.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案科目:初中数学 来源: 题型:解答题
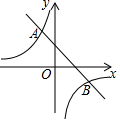 如图,一次函数y=k1x+b(k1≠0)与反比例函数y=$\frac{k_2}{x}$(k2≠0)的图象交于点A(-1,2),B(m,-1).
如图,一次函数y=k1x+b(k1≠0)与反比例函数y=$\frac{k_2}{x}$(k2≠0)的图象交于点A(-1,2),B(m,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
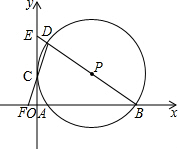 如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(-1,0),点D的坐标为(1,6).
如图,在平面直角坐标系中,⊙P经过y轴上一点C,与x轴分别相交于A、B两点,连接BP并延长分别交⊙P、y轴于点D、E,连接DC并延长交x轴于点F.若点F的坐标为(-1,0),点D的坐标为(1,6).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.
如图,一次函数y=kx+b与反比例函数y=$\frac{m}{x}$的图象交于A(1,4),B(4,n)两点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com