
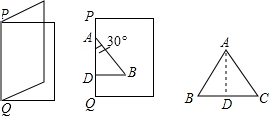
 如图,欢欢将一张白纸对折,折痕为PQ.以PQ上的线段AD为一条直角边画出直角三角形ABD,使∠DAB=30°,沿折线DBA剪下三角形纸片,将其打开展平,得到△ABC.
如图,欢欢将一张白纸对折,折痕为PQ.以PQ上的线段AD为一条直角边画出直角三角形ABD,使∠DAB=30°,沿折线DBA剪下三角形纸片,将其打开展平,得到△ABC. 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案科目:初中数学 来源: 题型:解答题
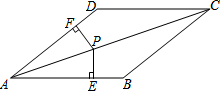 如图,在四边形ABCD中,AB∥CD,∠B=∠D.
如图,在四边形ABCD中,AB∥CD,∠B=∠D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a2×a5=a10 | B. | $\sqrt{a+b}=\sqrt{a}+\sqrt{b}$ | C. | (-a3)4=a12 | D. | $\sqrt{a^2}=a$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2cm,3cm,4cm | B. | 1cm,4cm,2cm | C. | 1cm,2cm,3cm | D. | 6cm,2cm,3cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
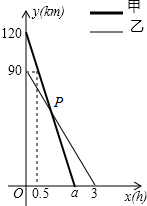 在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )
在一条笔直的公路旁依次有A、B、C三个村庄,甲、乙两人同时分别从A、B两村出发,甲骑摩托车,乙骑电动车沿公路匀速驶向C村,最终到达C村.甲、乙两人到C村的距离y1,y2(km)与行驶时间x(h)之间的函数关系如图所示,以下分析错误的是( )| A. | A、C两村间的距离为120km | |
| B. | 点P的坐标为(1,60) | |
| C. | 点P的意义表示经过1小时甲与乙相遇且距C村60km | |
| D. | 乙在行驶过程中,仅有一次机会距甲10km |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
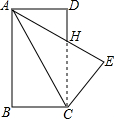 如图,矩形ABCD中,AB=4,BC=3,将矩形ABCD沿AC折叠,则重叠部分面积为( )
如图,矩形ABCD中,AB=4,BC=3,将矩形ABCD沿AC折叠,则重叠部分面积为( )| A. | $\frac{25}{8}$ | B. | $\frac{75}{8}$ | C. | $\frac{75}{16}$ | D. | $\frac{25}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com