练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    2．解方程组：
    （1）$\left\{\begin{array}{l}{x+y=5}\\{2x+y=8}\end{array}\right.$
    （2）$\left\{\begin{array}{l}{2x-5y=7}\\{3x+2y=1}\end{array}\right.$．

    分析 （1）方程组利用加减消元法求出解即可；
    （2）方程组利用加减消元法求出解即可．

    解答 解：（1）$\left\{\begin{array}{l}{x+y=5①}\\{2x+y=8②}\end{array}\right.$，
    ②-①得：x=3，
    把x=3代入①得：y=2，
    则方程组的解为$\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$；
    （2）$\left\{\begin{array}{l}{2x-5y=7①}\\{3x+2y=1②}\end{array}\right.$，
    ①×2+②×5得：19x=19，
    解得：x=1，
    把x=1代入①得：y=-1，
    则方程组的解为$\left\{\begin{array}{l}{x=1}\\{y=-1}\end{array}\right.$．

    点评 此题考查了解二元一次方程组，利用了消元的思想，消元的方法有：代入消元法与加减消元法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    12．解答下列各题：
    （1）计算：$\sqrt{（-\frac{5}{2}）^{2}}$-$\root{3}{-2\frac{10}{27}}$+（2017-π）0；
    （2）求x的值：$\frac{1}{2}$（x-2）3-32=0．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    13．解方程组：
    （1）$\left\{\begin{array}{l}{3（x-1）=y+5}\\{5（y-1）=3（x+5）}\end{array}\right.$
    （2）$\left\{\begin{array}{l}{\frac{x}{2}-\frac{x+1}{3}=1}\\{3x+2y=10}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

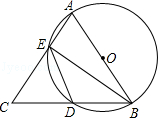    10．如图，△ABC中，AB=AC，以AB为直径的⊙O交AC，BC分别于点E，D两点，连结ED，BE．
    （1）求证：$\widehat{DE}$=$\widehat{BD}$．
    （2）若BC=6．AB=5，求BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，△ABC三个顶点的坐标分别为A（1，1），B（4，2），C（3，4）．
    （1）请画出将△ABC向左平移4个单位长度后得到的图形△A1B1C1
    （2）请画出将△ABC关于x轴对称的图形△A2B2C2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    7．如图，某人在山坡坡脚A处测得电视塔BC塔尖B的仰角为60°，沿山坡AM走到D处测得塔尖B的仰角为30°，已知AC为100米，山坡坡度i=1：3，C、A、E三点在同一直线上．求此人所在位置点D的铅直高度DE．（结果保留根号形式）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    14．计算：$\frac{-\sqrt{54}}{\sqrt{18}}$-$\frac{\sqrt{9}}{\sqrt{8}}$×$\sqrt{10}$+$\sqrt{12}$+$\sqrt{1\frac{1}{4}}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

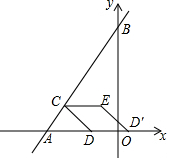    11．如图，在平面直角坐标系中，点A的坐标是（-3，0），点B的坐标是（0，4），动点C从点A出发沿射线AB方向以每秒1个单位的速度运动，过点C作CD⊥AB，交x轴于点D，点D关于y轴的对称点为D′，以DC，DD′为边作?CDD′E，设点C运动时间为t秒（t＞0）．
    （1）当D在线段AO上时，用含t的代数式表示DD′；
    （2）以AD为直径作⊙P，若点C在整个运动过程中，⊙P与△DD′E的边所在的直线相切，请求出所有满足条件的t的值；
    （3）连接BD，△ABD与?CDD′E重叠部分的面积记为S1，△CDD′E的面积为S2，若$\frac{{S}_{1}}{{S}_{2}}$＞$\frac{1}{4}$，求t的取值范围（直接写出答案）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    12．（1）计算：|-3|-（-1）2017-12×（$\frac{1}{3}$-$\frac{1}{4}$）+$\sqrt{25}$
    （2）已知，$\sqrt{a}$=3，$\root{3}{-b}$=2，试求$\sqrt{a+b}$的值．

    查看答案和解析>>

    同步练习册答案