
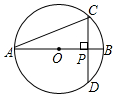
 如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若AB=4,AC=2$\sqrt{3}$,
如图,AB是⊙O的直径,弦CD⊥AB,垂足为点P,若AB=4,AC=2$\sqrt{3}$,分析 (1)连接CB,AC,由AB是⊙O的直径,得到∠ACB=90°;解直角三角形即可得到结论;
(2)解直角三角形得到CP=$\frac{1}{2}$AC=$\sqrt{3}$根据垂径定理即可得到结论;
(3)连接CO,OD,根据圆周角定理得到∠COD=120°,求得S扇形COD=$\frac{120•π×{2}^{2}}{360}$=$\frac{4}{3}$π,S△COD=$\frac{1}{2}$CD•OP=$\sqrt{3}$,于是得到结论.
解答  解:(1)连接CB,AC,
解:(1)连接CB,AC,
∵AB是⊙O的直径,
∴∠ACB=90°;
∴CB2=AB2-AC2=42-(2√3)2=16-12=4
∴CB=2=$\frac{1}{2}$AB
∴∠A=30°;
(2)∵∠A=30°,CD⊥AB,
∴CP=$\frac{1}{2}$AC=$\sqrt{3}$,
CD=2CP=AC=2$\sqrt{3}$;
(3)连接CO,OD,
∵CO=AO,
∴∠A=∠ACO=30°,∠COB=2∠A=60°,
∴∠COD=120°,
∴S扇形COD=$\frac{120•π×{2}^{2}}{360}$=$\frac{4}{3}$π,
∵OP=$\frac{1}{2}$OC=1,
∴S△COD=$\frac{1}{2}$CD•OP=$\sqrt{3}$,
∴弓形CBD的面积=S扇形COD-S△COD=$\frac{4}{3}$π-$\sqrt{3}$.
点评 此题考查了垂径定理、勾股定理以及扇形的面积的计算,注意掌握数形结合思想的应用.


 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:选择题
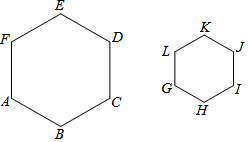
| A. | ∠B=2∠K | |
| B. | 六边形ABCDEF的周长=六边形GHIJKL的周长 | |
| C. | BC=2HI | |
| D. | S六边形ABCDEF=2S六边形GHIJKL |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{75}$ | B. | $5\sqrt{3}$ | C. | $\sqrt{2}$ | D. | $7\sqrt{3}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.
如图,在每个小正方形边长为1的方格纸中,△ABC的顶点都在方格纸格点上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com