Question

【题目】如图，是边长为1的等边三角形，是等腰直角三角形，且．

（1）求的长．

（2）连接交于点，求的值．

Answer 1

【答案】（1）（2）

【解析】

（1）已知BC=AB=AC=1，则在等腰直角△BCD中，由勾股定理即可求BC
（2）易证△ABD≌△ACD，从而得E点BC的中点，再根据等腰三角形的三线合一结合勾股定理即可求AE，DE，即可求得的值

解：（1）∵△ABC是边长为1的等边三角形，
∴BC=1
∵△BCD是等腰直角三角形，∠BDC=90°
∴由勾股定理：BC2=BD2+DC2，BD=DC 得，BC2=2BD2，则BD=

故BD的长为
（2）∵△ABC是边长为1的等边三角形，△BCD是等腰直角三角形
∴易证得△ABD≌△ACD（SSS）
∴∠BAE=∠CEA
∴E为BC中点，得BE=EC，AE⊥BC
∴在Rt△AEC中，由勾股定理得AE=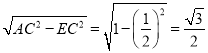
同理得ED=
∵AD=AE+ED
∴
故．