
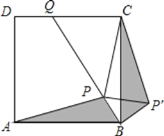
【题目】如图,点P是正方形ABCD内一点,点P到点A,B和C的距离分别为![]() ,1,2
,1,2![]() ,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为______ (度)
,△ABP绕点B旋转至△CBP′,连结PP′,并延长BP与DC相交于点Q,则∠CPQ的大小为______ (度)
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中, △ABC如图(每个小正方形的边长均为1).

(1)请画出△ABC沿x轴向右平移4个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标:A′(____,_____); B′(____,_____);C′(____,_____).
(3)求△A′B′C′的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,AH⊥BC于点H,过点C作CD⊥AC,连接AD,点M为AC上一点,且AM=CD,连接BM交AH于点N,交AD于点E.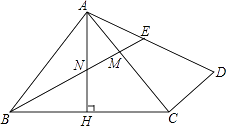
(1)若AB=3,AD= ![]() ,求△BMC的面积;
,求△BMC的面积;
(2)点E为AD的中点时,求证:AD= ![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为K90的化学赛道,其中助滑坡AB长90米,坡角a=40°,一个曲面平台BCD连接了助滑坡AB与着陆坡,某运动员在C点飞向空中,几秒之后落在着陆坡上的E处,已知着陆坡DE的坡度i=1: ![]() ,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)
,此运动员成绩为DE=85.5米,BD之间的垂直距离h为1米,则该运动员在此比赛中,一共垂直下降了( )米.(参考数据:sin40°≈0.64,cos40°≈0.76,tan40°≈0.84,结果保留一位小数)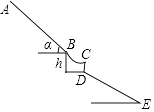
A.101.4
B.101.3
C.100.4
D.100.3
查看答案和解析>>
科目:初中数学 来源: 题型:
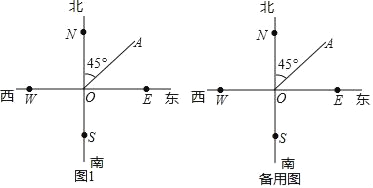
【题目】如图,射线ON、OE、OS、OW分别表示从点O出发北、东、南、西四个方向,点A在点O的北偏东45°方向,点B在点O的北偏西30°方向.
(1)画出射线OB,若∠BOC与∠AOB互余,请在图1或备用图中画出∠BOC;
(2)若OP是∠AOC的角平分线,直接写出∠AOP的度数(不需要计算过程).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明.
已知,如图所示,BCE,AFE是直线,
AB∥CD,∠1=∠2,∠3=∠4.
求证:AD∥BE
证明:∵ AB∥CD (已知)
∴ ∠4 =∠ ( )
∵ ∠3 =∠4 (已知)
∴ ∠3 =∠ ( )
∵∠1 =∠2 (已知)
∴∠1+∠CAF =∠2+ ∠CAF ( )
即:∠ =∠ .
∴ ∠3 =∠ ( )
∴ AD∥BE ( )

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,分别以AB、AC、BC为边在BC的同侧作等边△ABD,等边△ACE、等边△BCF.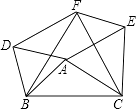
(1)求证:四边形DAEF是平行四边形;
(2)探究下列问题:(只填满足的条件,不需证明)
①当△ABC满足条件时,四边形DAEF是矩形;
②当△ABC满足条件时,四边形DAEF是菱形;
③当△ABC满足条件时,以D、A、E、F为顶点的四边形不存在.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥CD,AC平分∠BAD,CE∥AD交AB于E.
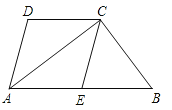
(1)求证:四边形AECD是菱形;
(2)若点E是AB的中点,试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】暑假期间,小明一家到某拓展基地训练,![]() 小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发
小明和他妈妈坐公交车先出发,爸爸在家整理物品,随后爸爸自驾车沿着相同的道路后出发![]() 他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地
他爸爸到拓展基地后,发现忘了东西在家里,于是立即返回家里取,取到东西后又马上驾车前往拓展基地![]() 如图是他们离家的距离s
如图是他们离家的距离s![]() km
km![]() 与小明离家的时问t
与小明离家的时问t![]() 的关系图.
的关系图.
(1)请根据图象,回答问题:
①图中点A表示的意义是 .
②当爸爸第一次到达度假村后,小明离度假村的距离是______ km;
(2)爸爸在返回家的途中与小明相遇时,小明离家的距离是多少?
(3)整个运动过程中(双方全部到达会合时,视为运动结束),请直接写出小明与爸爸相距24km时t的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com