
【题目】如图有一座抛物线形拱桥,桥下面在正常水位是AB宽20m,水位上升3m就达到警戒线CD,这是水面宽度为10m。

(1)在如图的坐标系中求抛物线的解析式。
(2)若洪水到来时,水位以每小时0.2m的速度上升,从警戒线开始,再持续多少小时才能到拱桥顶?
【答案】![]() 5小时
5小时
【解析】试题分析:(1)首先设所求抛物线的解析式为:y=ax2(a≠0),再根据题意得到C(-5,-1),利用待定系数法即可得到抛物线解析式;
(2)根据抛物线解析式计算出A点坐标,进而得到F点坐标,然后计算出EF的长,再算出持续时间即可.
试题解析:(1)设所求抛物线的解析式为:y=ax2(a≠0),
∵由CD=10m,CD到拱桥顶E的距离仅为1m,
则C(-5,-1),
把C的坐标分别代入y=ax2得:a=-![]() ,
,
故抛物线的解析式为y=-![]() x2;
x2;
(2)如图:
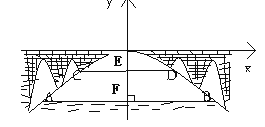
∵AB宽20m,
∴设A(-10,b),
把A点坐标代入抛物线的解析式为y=-![]() x2中,
x2中,
解得:b=-4,
∴F(0,-4),
∴EF=3,
∵水位以每小时0.3m的速度上升,
∴3÷0.3=10(小时),
答:从正常水位开始,持续10小时到达警戒线.


科目:初中数学 来源: 题型:
【题目】科学家在实验中测出某种微生物细胞直径约为0.00000309米,把0.00000309用科学记数法表示为( )
A. 3.09×10﹣6B. 3.09×10﹣5C. 3.09×106D. 3.09×105
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某机构对2016年微信用户的职业颁布进行了随机抽样调查(职业说明:A:党政机关、军队,B:事业单位,C:企业,D:自由职业及人体户,E:学生,F:其他),图1和图2是根据调查数据绘制而成的不完整的统计图.请根据图中提供的信息,解答下列问题:

(1)该机构共抽查微信用户___________人;
(2)在图.1中,补全条形统计图;
(3)在图2中,“D”用户所对应扇形的圆心角度数为___________度;
(4)2016年微信用户约有7.5亿人,估计“E”用户大约有________亿人.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com