阅读下面材料,完成相应的填空:
(1)双循环与单循环问题:
小田是个足球迷,他发现有的比赛是单循环的,就是每两个球队之间只赛一场;有的比赛是双循环的,每两个球队按主客场要赛两场,同时小田又是个数学迷,他想探究如果有n(n≥2)个球队进行双循环比赛,一共要赛多少场?
①小田觉得从特殊情况入手可能会找到灵感,于是他取n=2,要赛2场;n=3,赛6场;n=4,赛12场;那么n=5,要赛________场…,由此得出,n(n≥2)个球队进行双循环比赛,一共要赛________场.
②聪明的小田由①中的结论,很快地得出n(n≥2)个球队单循环比赛场数为________;
(2)知识迁移:①平面内有10个点,且任意3个点不在同一条直线上,经过每两点画一条直线,一共能画________条不同的直线.②一个n边形(n≥3)有________条对角线.
解:(1)①当n=5时,每支球队与另外4支队伍比赛,共有4×5=20场比赛;
n支球队每支球队与其余队伍比赛n-1场,共有n(n-1);
②单循环则为

;
(2)①当平面上有2个点时,可以画
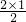
=
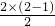
条直线;
当平面上有3个点时,可以画

=

=3条直线;
…
当平面上有n(n≥2)个点时,可以画

条直线;
因此当n=10时,一共可以画(10×9)÷2=45条直线.
②过n边形(n≥3)的一个顶点可以作(n-3)条对角线,
这个n边形共有

条对角线.
故答案为:20,

;45,

.
分析:(1)①n支球队举行双循环比赛,由于每一球队都要比赛(n-1)场,又每两个球队按主客场要赛两场,所以n(n≥2)个球队一共要赛 n(n-1)场;
②由于是单循环比赛,每两个球队之间只赛一场,则共比赛

;
(2)①根据第(1)题可知当n=10时,一共可以画(10×9)÷2=45条直线;
②从n边形的一个顶点出发,能引出(n-3)条对角线,一共有

条对角线.
点评:此题是一道探求规律题,考查了数字的变化类问题,解题的关键是读懂题意,找出规律,并应用得到的规律解决实际问题.

 ;
;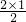 =
=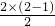 条直线;
条直线; =
= =3条直线;
=3条直线; 条直线;
条直线; 条对角线.
条对角线. ;45,
;45, .
. ;
; 条对角线.
条对角线.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案