
����Ŀ��������һ�����⣺̽������y= ![]() ��ͼ�������ʣ� ������С�ĵ�̽�����̣��벹��������
��ͼ�������ʣ� ������С�ĵ�̽�����̣��벹��������
��1������y= ![]() ���Ա���x��ȡֵ��Χ����
���Ա���x��ȡֵ��Χ����
��2�������y��x�ļ����Ӧֵ��
x | �� | ��3 | ��2 | ��1 | 0 | 2 | 3 | 4 | 5 | �� |
y | �� | �� | �� | �� | 0 | 2 | | | | �� |
��ͼ����ƽ��ֱ������ϵxOy�У���������ϱ��и��Զ�ӦֵΪ����ĵ㣮
�ٹ۲�ͼ�и����λ�÷��֣���A1��B1 �� A2��B2 �� A3��B3 �� A4��B4������ij�����ĶԳƣ���õ������Ϊ��
��С�ķ�������y= ![]() �ı���ʽ���֣���x��1ʱ���ú��������ֵΪ0����ú���ͼ����ֱ��x=1������ߵ������Ϊ��
�ı���ʽ���֣���x��1ʱ���ú��������ֵΪ0����ú���ͼ����ֱ��x=1������ߵ������Ϊ��
��3��С�IJ����˸ú���ͼ���������㣨 ![]() ����
���� ![]() ������
������ ![]() ��
�� ![]() ���� ������ͼ������������㣬�������ú�����ͼ��
���� ������ͼ������������㣬�������ú�����ͼ��
��д���ú�����һ�����ʣ� ��
���𰸡�
��1��x��1
��2����1��1������0��0��
��3�� ����x��1ʱ���ú�������СֵΪ1
����x��1ʱ���ú�������СֵΪ1
���������⣺��1��������ã�2x��2��0�����x��1���ʴ��ǣ�x��1����2���ٵ�A1��B1 �� A2��B2 �� A3��B3 �� A4��B4������ij�����ĶԳƣ�A1��0��0����B2��2��2���������ĵ������Ϊ��1��1�����ڡߵ�x��1ʱ���ú��������ֵΪ0�� ��ú���ͼ����ֱ��x=1������ߵ������Ϊ��0��0�������Դ��ǣ�1��1������0��0������3���ڸú��������ʣ���������x��0ʱ��y��x�����������
��0��x��1ʱ��y��x���������С����1��x��2ʱ��y��x���������С��
��x��2ʱ��y��x���������������������ͼ����һ�����������ޣ�
������������ͼ����ֱ��x=1���㣬ͼ������������ɣ���������x��1ʱ���ú�������СֵΪ1�����Դ��ǵ�x��1ʱ���ú�������СֵΪ1��
�����㾫����ͨ��������ö��κ�����ͼ��Ͷ��κ��������ʣ����ն��κ���ͼ��ؼ��㣺1�����ڷ���2���Գ��� 3������ 4����x�ύ�� 5����y�ύ�㣻�����ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С�����Խ����⣮


 ��ѧ����ϵ�д�
��ѧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�DZ߳�Ϊm���������Σ�D��E��F�ֱ��ڱ�AB��BC��CA�ϣ�AE��BF���ڵ�P��BF��CD���ڵ�Q��CD��AE���ڵ�R���� ![]() =
= ![]() =
= ![]() =k��0��k��
=k��0��k�� ![]() ����
����
��1�����PQR�Ķ�����
��2����֤����ARD�ס�ABE��
��3�����PQR���ABC�����֮�ȣ��ú�k�Ĵ���ʽ��ʾ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1����P��Q�ֱ��DZ߳�Ϊ4cm�ĵȱ���ABC��AB��BC�ϵĶ��㣬��P�Ӷ���A����Q�Ӷ���Bͬʱ�����������ǵ��ٶȶ�Ϊ1cm��s��
������AQ��CP���ڵ�M���ڵ�P��Q�˶��Ĺ����У���CMQ�Ĵ�С�仯�����仯����˵�����ɣ������䣬��ֱ��д�����Ķ�����
�Ƶ�P��Q���˶������У����˶�ʱ��Ϊt����tΪ��ֵʱ����PBQΪֱ�������Σ�
����ͼ2������P��Q���˶����յ�����������AB��BC���˶���ֱ��AQ��CP����ΪM�����CMQ�Ĵ�С�仯����˵�����ɣ������䣬��������Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����D��BC���е㣬DE��ֱƽ��AC������ΪE��F��BA���е㣮��֤��DF��AB�Ĵ�ֱƽ���ߣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
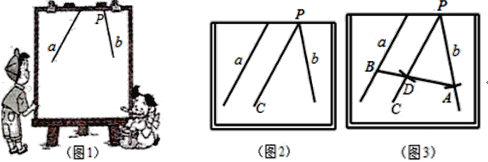
����Ŀ��С�������α��е�һ���⣺��ͼ1��ֱ��a��b���ɵĽ��ܵ���������ȥ�ˣ�����ʲô�취����������ֱ�����ɵĽǵĶ�����С���������ǣ���ͼ2����PC��a������ֱ��b��PC�ļнǶ�������ֱ��a��b���ɽǵĶ�����
��1����д���������������ɣ�
��2��С���ڴ˻������ֽ��������²�����̽������ͼ3����
����PΪԲ�ģ����ⳤΪ�뾶��Բ�����ֱ�ֱ��b��PC�ڵ�A��D��
������AD���ӳ���ֱ��a�ڵ�B����ֱ��д��ͼ3���������PAB��ȵĽǣ�
��3������ͼ3������������ֱ��a��b���ɵ��ܵ���������ȥ�Ľ�����ƽ���ߣ������ڵIJ��֣���ֻҪ������ͼ�Σ���������ͼ�ۼ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У���P��QΪij���������ڵ��������㣬�Ҹ����ε������Խ��߷ֱ���x�ᣬy��ƽ�У���Ƹ�����Ϊ��P��Q�ġ�������Ρ���ͼ1Ϊ��P��Q�ġ�������Ρ���һ��ʾ��ͼ�� 
��֪��A������Ϊ��1��4������B������Ϊ��b��0����
��1����b=3����R����1��0����S��5��4����T��6��4�����ܹ���Ϊ��A��B�ġ�������Ρ����������
��2������A��B�ġ�������Ρ�Ϊ�����Σ���b��ֵ��
��3����B�İ뾶Ϊ ![]() ����C������Ϊ��2��4��������B�ϴ��ڵ�M�����߶�AC�ϴ��ڵ�N��ʹ��M��N�ġ�������Ρ�Ϊ�����Σ���ֱ��д��b��ȡֵ��Χ��
����C������Ϊ��2��4��������B�ϴ��ڵ�M�����߶�AC�ϴ��ڵ�N��ʹ��M��N�ġ�������Ρ�Ϊ�����Σ���ֱ��д��b��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����x��һԪ���η���3x2��kx+k��4=0��
��1���жϷ��̸��������
��2�����˷�����һ������������ѡ��һ�����ʵ�kֵ���������ʱ���̵ĸ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ� ���ڷ�չʱ���硢��չ�ٶȿ죬����20������ģ�ĸ��ٿ������裬�����Ļ��ڣ������廷�ڿɹ����������������ԴԽ��Խϡȱ����������ع�Ӧ���������廷�⣬�����������Զ�����أ�
���й�������2017��2�±���������ij�г��о�Ժ������ͳ�ƣ�2016�꣬���˱��Ϸ����ڱ����½���Ʒסլ��������������֮ʱ��������������½���Ʒסլ���������������е������У���ƽ��ͨ�ݡ����������������ǡ����������µ�����������Ϊ���������½���Ʒסլ�ɽ�����2015���½���46.82%�������졢���ơ����ᡢƽ�ȡ���ͷ������ɽ��˳�塢���ˡ�ʯ��ɽ����̨ʮ�����½���Ʒסլ�ɽ�������Ϊ���ǣ��Ƿ�����Ϊ˳��������2015��������118.80%�����⣬�ӻ��߳ɽ�����ռ�������ϣ�ͬ�����Կ����ɽ����������������ƣ�����ͳ�ƣ�2008�굽2016�꣬����ȫ�гɽ����½���Ʒסլ�У��������ڵ�ռ����3.0%�½�����0.2%����������֮���ռ�ȴ�5.7%�½�����0.8%�������Ļ�֮���ռ�ȴ�12.3%�½�����2.3%���ġ��廷֮���ռ�ȴ�21.9%�½�����4.4%��Ҳ����˵������ɽ���λ���廷֮�ڵ��·�ռ�ȣ���2008���42.8%�½�����2016���7.7%���»����Ʒdz����ԣ��ɴ˿ɼ����·��г���Զ�����DZ������ز��г���չ�Ĵ�����������ע��ռ�ȣ�ָ����������ռ�ı��أ����ðٷֱȱ�ʾ��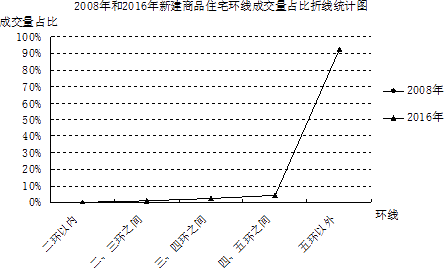
�������ϲ��Ͻ���������⣺
��1����ȫ����ͳ��ͼ��
��2�����ݲ����ṩ����Ϣ��Ԥ�� 2017��λ�ڱ������廷֮���½���Ʒסլ�ɽ���ռ��Լ �� ���Ԥ�������� ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ� ��������������ָ��ҵ��������������У������վ�㡢����վ�㡢����������ҵ�����������������ṩ���г�������һ�ַ����ǹ������õ�һ������̬�����������ij����ø�����û����˸��õĴ���ѡ�����г�Ҳ������һ���ֹ�����ͨ�����ij��У�
Quest Mobile����M����O�͵�����2016��10�©���2017��1�µ��¶��û�ʹ����������ʾ��
�������ϲ��Ͻ���������⣺
��1����ϸ�Ķ��ϱ�����O�͵������û���������ͼ��ʾ����������ͼ�б�����Ӧ���ݣ�
��2������ͼ�������ṩ�����ݣ�ѡ����������Ȥ�ķ��棬д��һ���㷢�ֵĽ��ۣ�
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com