
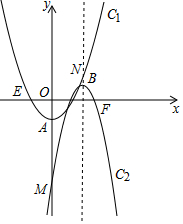
 如图,抛物线C1:y1=tx2-1(t>0)和抛物线C2:y2=-4(x-h)2+1(h≥1).
如图,抛物线C1:y1=tx2-1(t>0)和抛物线C2:y2=-4(x-h)2+1(h≥1).分析 (1)根据顶点时的抛物线解析式,可得顶点坐标;
(2)根据平行四边形的判定:一组对边平行且相等的四边形是平行四边形,可得关于t的方程,根据解方程,可得答案;
(3)根据二次项的系数互为相反数,可得顶点的纵坐标互为相反数,两抛物线成中心对称,根据相似三角形的判定与性质,可得关于t的方程,根据解方程,可得答案.
解答 解:(1)抛物线C1:y1=tx2-1的顶点坐标是(0,-1),
抛物线C2:y2=-4(x-h)2+1的顶点坐标是(h,1),
故答案为:(0,-1),(h,1);
(2)∵AM∥BN,
∴当AM=BN时,A、B、M、N为顶点的四边形是平行四边形,
∵当x=h时,y1=1,y2=tx2-1=th2-1,
∴PN=|1-(th2-1)\=|2-th2|.
①当点B在点A的下方时,4h2-2=th2-2,∵h2≠0,∴t=4;
②当点B在点A的上方时,4h2-2=2-th2,整理,得t+4=$\frac{4}{{h}^{2}}$,
∵t>0时,t+4>4;当h≥1时,$\frac{4}{{h}^{2}}$≤4,
∴这样的t值不存在,
答:当点B在点A的下方时,t=4,当点B在点A的上方时不存在;
(3)由(2)可知,二次项系数互为相反数,
∴两抛物线的形状相同,故它们成中心对称,
∵点A和点B的纵坐标的绝对值相同,
∴两抛物线得对称中心落在x轴上.
∵四边形AEBF是平行四边形,
∴当∠EAF=90°时,四边形AFBE是矩形,
∵抛物线C1与x轴左交点坐标是(-$\frac{1}{2}$,0),
∴OE=$\frac{1}{2}$.
∵抛物线C2与x轴右交点坐标是(h+$\frac{1}{2}$,0)且h≥1,
∴OF=h+$\frac{1}{2}$.
∵∠FAO+∠EAO=90°,∠EAO+AEO=90°,
∴∠FAO=∠AEO,
又∵∠FOA=∠EOA=90°,
∴△AEO∽△FAO,$\frac{AO}{OE}$=$\frac{OF}{AO}$
∴OA2=OE•OF,即$\frac{1}{2}$(h+$\frac{1}{2}$)=1,解得h=$\frac{3}{2}$>1,
∴四边形AEBF能为矩形,且h的值为$\frac{3}{2}$.
点评 本题考查了二次函数综合题,解(1)的关键是利用顶点式解析式得出顶点坐标;解(2)的关键是利用平行四边形的判定得出关于t的方程,要分类讨论,以防遗漏;解(3)的关键是利用相似三角形的判定与性质得出关于h的方程.


科目:初中数学 来源: 题型:选择题
| A. |  | B. |  | ||
| C. | 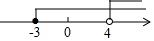 | D. |  |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
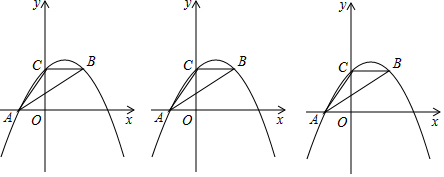
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )
如图,△ABC的三个顶点的坐标分别为A(-3,5),B(-3,0),C(2,0),将△ABC绕点B顺时针旋转一定角度后使A落在y轴上,与此同时顶点C恰好落在y=$\frac{k}{x}$的图象上,则k的值为( )| A. | -2 | B. | -3 | C. | -4 | D. | -5 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
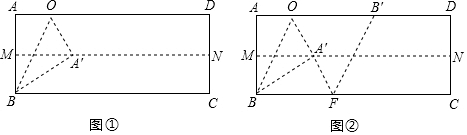
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com