
【题目】已知:如图所示,△ABC中,∠BAC=90°,AB=AC,分别过点B、C作经过点A的直线L的垂线段BD、CE,垂足分别D、E. 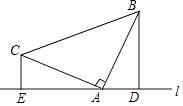
(1)求证:DE=BD+CE.
(2)如果过点A的直线经过∠BAC的内部,那么上述结论还成立吗?请给出你的结论,并画出图形予以证明.
【答案】
(1)解:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=90°,
∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
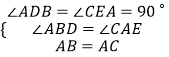 ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD+AE=DE,
∴BD+CE=DE;
(2)解:上述结论不成立.
如图所示,BD=DE+CE.
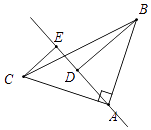
证明:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=90°,
∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
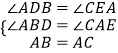 ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AD+DE=AE,
∴BD=DE+CE.
如图所示,CE=DE+BD,
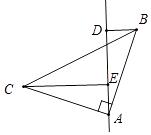
证明:证明:∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵BD⊥l,CE⊥l,
∴∠ADB=∠CEA=90°,
∴∠BAD+∠ABD=90°,
∴∠ABD=∠CAE.
在△ABD和△CAE中,
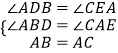 ,
,
∴△ABD≌△CAE(AAS),
∴BD=AE,AD=CE,
∵AE+DE=AD,
∴CE=DE+BD.
【解析】(1)由垂线的定义和角的互余关系得出∠BDA=∠CEA=90°,∠ABD=∠CAE,由AAS证明△ABD≌△CAE,得出对应边相等BD=AE,AD=CE,由AD+AE=DE,即可得出结论;(2)由垂线的定义和角的互余关系得出∠ADB=∠CEA=90°,∠ABD=∠CAE,由AAS证明△ABD≌△CAE,得出对应边相等BD=AE,AD=CE,由AE、DE、AD之间的和差关系,即可得出结论.
【考点精析】认真审题,首先需要了解等腰直角三角形(等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°).


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
【题目】实验探究
(1)探究发现 数学活动课上,小明说“若直线y=2x﹣1向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”
经过一番讨论,小组成员展示了他们的解答过程:
在直线y=2x﹣1上任取点A(0,﹣1),
向左平移3个单位得到点A′(﹣3,﹣1)
设向左平移3个单位后所得直线所对应的函数表达式为y=2x+n.
因为y=2x+n过点A′(﹣3,﹣1),
所以﹣6+n=﹣1,
所以n=5,
填空:所以平移后所得直线所对应函数表达式为
(2)类比运用 已知直线y=2x﹣1,求它关于x轴对称的直线所对应的函数表达式;
(3)拓展运用 将直线y=2x﹣1绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】掷一枚正方体的骰子,各个面上分别标有数字1, 2,3,4,5,6,求下列事件发生的频率的大小:
①朝上的数字是奇数;
②朝上的数字能被3除余1;
③朝上的数字不是3的倍数;
④朝上的数字小于6;
⑤朝上的数字不小于3.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形ABCD中,E、F分别在AD、DC上,∠ABE=∠CBF=15°,G是AD上另一点,且∠BGD=120°,连接EF、BG、FG、EF、BG交于点H,则下面结论:①DE=DF;②△BEF是等边三角形;③∠BGF=45°;④BG=EG+FG中,正确的是(请填番号) 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地区林业局要考察一种树苗移植的成活率,对该地区这种树苗移植成活的情况进行调查统计,并绘制了如图所示的统计图,根据统计图提供的信息解决下列问题:

(1)这种树苗成活的频率稳定在___________,成活的概率估计值为___________.
(2)该地区已经移植这种树苗5万棵.
①估计这种树苗成活___________万棵.
②如果该地区计划成活18万棵这种树苗,那么还需移植这种树苗约多少万棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△A'B'C'关于直线l对称.

(1)△ABC____△A'B'C';
(2)A点的对应点是____,C'点的对应点是____;
(3)连接BB'交l于点M,连接AA'交l于点N,则BM=____,AA'与BB'的位置关系是____;
(4)直线l____AA'.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com