
| A. | $\frac{1001}{2004}$ | B. | $\frac{1001}{1002}$ | C. | $\frac{2004}{2005}$ | D. | $\frac{1002}{2005}$ |
分析 当x=0时,y=$\frac{1}{k+1}$,当y=0时,x=$\frac{1}{k}$,所以面积S=$\frac{1}{2}•\frac{1}{k}•\frac{1}{k+1}=\frac{1}{2}(\frac{1}{k}-\frac{1}{k+1})$,根据规律代入数据可求出值.
解答 解:∵x=0,y=$\frac{1}{k+1}$,y=0,x=$\frac{1}{k}$.
∴面积S=$\frac{1}{2}•\frac{1}{k}•\frac{1}{k+1}=\frac{1}{2}(\frac{1}{k}-\frac{1}{k+1})$,
∴S1+S2+…+S2004=$\frac{1}{2}•(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+…+\frac{1}{2004}-\frac{1}{2005})=\frac{1002}{2005}$.
故选D.
点评 本题主要考查了一次函数图象上的点的坐标特点,考查找规律的能力,关键能看分式的特点.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:初中数学 来源: 题型:选择题
| A. | x为任意实数 | B. | 2≤x≤4 | C. | x≥4 | D. | x≤2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0.15 | B. | 0.10 | C. | 0.20 | D. | 0.30 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
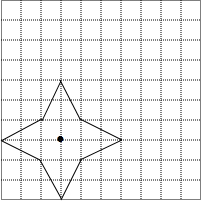 如图,一朵四瓣花飘动在10×10的网格中.
如图,一朵四瓣花飘动在10×10的网格中.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com